Advertisements
Advertisements
प्रश्न
If two straight lines intersect each other, prove that the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angle.
उत्तर
Let AB and CD intersect at a point O
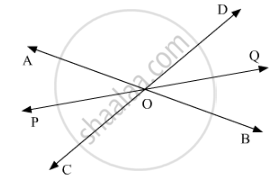
Also, let us draw the bisector OP of ∠AOC.
Therefore,
∠AOP = ∠POC (1)
Also, let’s extend OP to Q.
We need to show that, OQ bisects ∠BOD.
Let us assume that OQ bisects∠BOD, now we shall prove that POQ is a line.
We know that,
∠AOCand ∠DOBare vertically opposite angles. Therefore, these must be equal, that is:
∠AOC = ∠DOB (2)
∠AOPand ∠BOQ are vertically opposite angles. Therefore,
∠AOP = ∠BOQ
Similarly,
∠POC = ∠DOQ
We know that:
∠AOP +∠AOD+∠DOQ+∠POC+∠BOC+∠BOQ = 360°
2∠AOP+∠AOD+2∠DOQ+∠BOC =360°
2∠AOP + 2∠AOD+ 2∠DOQ = 360°
2(∠AOP+∠AOD+ ∠DOQ) = 360°
∠AOP+∠AOD+ ∠DOQ = `(360°)/2`
∠AOP+∠AOD+ ∠DOQ = 180°
Thus, POQ is a straight line.
Hence our assumption is correct. That is,
We can say that if the two straight lines intersect each other, then the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angles.
APPEARS IN
संबंधित प्रश्न
If an angle is 30° more than one half of its complement, find the measure of the angle.
In below fig, determine the value of x.

The supplement of an acute angle is .................
In the given figure, AB || CD || EF and GH || KL. The measure of ∠HKL is

State, true or false:
Is 45° the supplement of 45°?
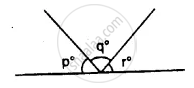
In the given figure. p° = q° = r°, find each.
Write the complement of 25°
Write the complement of `1/2` of a right angle
Write the supplement of `1/5` of a right angle
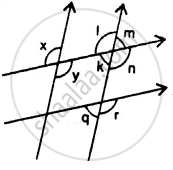
In the given figure, the arrows indicate parallel lines. State which angles are equal. Give a reason.