Advertisements
Advertisements
प्रश्न
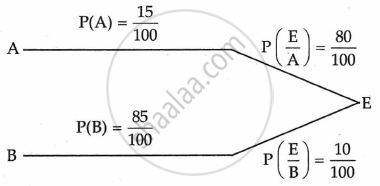
In a company, 15% of the employees are graduates and 85% of the employees are non-graduates. As per the annual report of the company, 80% of the graduate employees and 10% of the non-graduate employees are in the Administrative positions. Find the probability that an employee selected at random from those working in administrative positions will be a graduate.
उत्तर
Let A = Employees are graduates
B = Employees are non-graduates
and E = Working in administrative positions
Given P(A) = `15/100`,
P(B) = `85/100`
`P(E/A) = 80/100`,
`P(E/B) = 10/100`
By Bayes' theorem,
`P(A/E) = (P(A)*P(E/A))/(P(A)*P(E/A) + P(B)*P(E/B))`
`P(A/E) = (15/100 xx 80/100)/(15/100 xx 80/100 + 85/100 xx 10/100)`
= `(15 xx 80)/(15 xx 80 + 85 xx 10)`
= `1200/(1200 + 850)`
= `1200/2050`
= `120/205`
= `24/41`
APPEARS IN
संबंधित प्रश्न
There are three coins. One is two headed coin (having head on both faces), another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?
Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 or 4 with the die?
Two groups are competing for the positions of the Board of Directors of a Corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.
A factory has three machines X, Y and Z producing 1000, 2000 and 3000 bolts per day respectively. The machine X produces 1% defective bolts, Y produces 1.5% and Zproduces 2% defective bolts. At the end of a day, a bolt is drawn at random and is found to be defective. What is the probability that this defective bolt has been produced by machine X?
An insurance company insured 3000 scooters, 4000 cars and 5000 trucks. The probabilities of the accident involving a scooter, a car and a truck are 0.02, 0.03 and 0.04 respectively. One of the insured vehicles meet with an accident. Find the probability that it is a (i) scooter (ii) car (iii) truck.
A manufacturer has three machine operators A, B and C. The first operator A produces 1% defective items, whereas the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job for 30% of the time and C on the job for 20% of the time. A defective item is produced. What is the probability that it was produced by A?
An item is manufactured by three machines A, B and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on machine A, 30% on Band 20% on C. 2% of the items produced on A and 2% of items produced on B are defective and 3% of these produced on C are defective. All the items stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
An insurance company insured 2000 scooters and 3000 motorcycles. The probability of an accident involving a scooter is 0.01 and that of a motorcycle is 0.02. An insured vehicle met with an accident. Find the probability that the accidented vehicle was a motorcycle.
In a factory, machine A produces 30% of the total output, machine B produces 25% and the machine C produces the remaining output. If defective items produced by machines A, B and C are 1%, 1.2%, 2% respectively. Three machines working together produce 10000 items in a day. An item is drawn at random from a day's output and found to be defective. Find the probability that it was produced by machine B?
For A, B and C the chances of being selected as the manager of a firm are in the ratio 4:1:2 respectively. The respective probabilities for them to introduce a radical change in marketing strategy are 0.3, 0.8 and 0.5. If the change does take place, find the probability that it is due to the appointment of B or C.
Three persons A, B and C apply for a job of Manager in a Private Company. Chances of their selection (A, B and C) are in the ratio 1 : 2 :4. The probabilities that A, B and C can introduce changes to improve profits of the company are 0.8, 0.5 and 0.3, respectively. If the change does not take place, find the probability that it is due to the appointment of C.
Of the students in a college, it is known that 60% reside in a hostel and 40% do not reside in hostel. Previous year results report that 30% of students residing in hostel attain A grade and 20% of ones not residing in hostel attain A grade in their annual examination. At the end of the year, one students is chosen at random from the college and he has an A grade. What is the probability that the selected student is a hosteler?
Coloured balls are distributed in four boxes as shown in the following table:
| Box | Colour | |||
| Black | White | Red | Blue | |
| I II III IV |
3 2 1 4 |
4 2 2 3 |
5 2 3 1 |
6 2 1 5 |
A box is selected at random and then a ball is randomly drawn from the selected box. The colour of the ball is black, what is the probability that ball drawn is from the box III.
If a machine is correctly set up it produces 90% acceptable items. If it is incorrectly set up it produces only 40% acceptable item. Past experience shows that 80% of the setups are correctly done. If after a certain set up, the machine produces 2 acceptable items, find the probability that the machine is correctly set up.
A is known to speak truth 3 times out of 5 times. He throws a die and reports that it is one. Find the probability that it is actually one.
A speaks the truth 8 times out of 10 times. A die is tossed. He reports that it was 5. What is the probability that it was actually 5?
In answering a question on a multiple choice test a student either knows the answer or guesses. Let \[\frac{3}{4}\] be the probability that he knows the answer and \[\frac{1}{4}\] be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability \[\frac{1}{4}\]. What is the probability that a student knows the answer given that he answered it correctly?
There are three bags, each containing 100 marbles. Bag 1 has 75 red and 25 blue marbles. Bag 2 has 60 red and 40 blue marbles and Bag 3 has 45 red and 55 blue marbles. One of the bags is chosen at random and a marble is picked from the chosen bag. What is the probability that the chosen marble is red?
(Activity):
Mr. X goes to office by Auto, Car, and train. The probabilities him travelling by these modes are `2/7, 3/7, 2/7` respectively. The chances of him being late to the office are `1/2, 1/4, 1/4` respectively by Auto, Car, and train. On one particular day, he was late to the office. Find the probability that he travelled by car.
Solution: Let A, C and T be the events that Mr. X goes to office by Auto, Car and Train respectively. Let L be event that he is late.
Given that P(A) = `square`, P(C) = `square`
P(T) = `square`
P(L/A) = `1/2`, P(L/C) = `square` P(L/T) = `1/4`
P(L) = P(A ∩ L) + P(C ∩ L) + P(T ∩ L)
`="P"("A")*"P"("L"//"A") + "P"("C")*"P"("L"//"C") + "P"("T")*"P"("L"//"T")`
`= square * square + square * square + square * square`
`= square + square + square`
`= square`
`"P"("C"//"L") = ("P"("L" ∩ "C"))/("P"("L"))`
= `("P"("C") * "P"("L"//"C"))/("P"("L"))`
`= (square * square)/square`
`= square`
Solve the following:
The chances of P, Q and R, getting selected as principal of a college are `2/5, 2/5, 1/5` respectively. Their chances of introducing IT in the college are `1/2, 1/3, 1/4` respectively. Find the probability that IT is introduced by Q
Solve the following:
In a factory which manufactures bulbs, machines A, B and C manufacture respectively 25%, 35% and 40% of the bulbs. Of their outputs, 5, 4 and 2 percent are respectively defective bulbs. A bulbs is drawn at random from the product and is found to be defective. What is the probability that it is manufactured by the machine B?
Suppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed 30% of the people have blood group O. If a left handed person is selected at random, what is the probability that he/she will have blood group O?
Refer to Question 41 above. If a white ball is selected, what is the probability that it came from Bag 3
A letter is known to have come either from TATA NAGAR or from CALCUTTA. On the envelope, just two consecutive letter TA are visible. What is the probability that the letter came from TATA NAGAR.
In a bolt factory, machines X, Y and Z manufacture 20%, 35% and 45% respectively of the total output. Of their output 8%, 6% and 5% respectively are defective bolts. One bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured in machine Y?
A jewellery seller has precious gems in white and red colour which he has put in three boxes.
The distribution of these gems is shown in the table given below:
| Box | Number of Gems | |
| White | Red | |
| I | 1 | 2 |
| I | 2 | 3 |
| III | 3 | 1 |
He wants to gift two gems to his mother. So, he asks her to select one box at random and pick out any two gems one after the other without replacement from the selected box. The mother selects one white and one red gem.
Calculate the probability that the gems drawn are from Box II.
