Advertisements
Advertisements
प्रश्न
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French and English but not Sanskrit
उत्तर
Let us use Venn diagram method.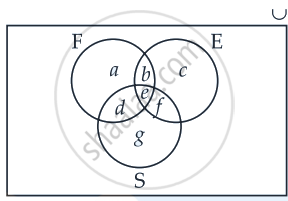
Total number of students = 50
⇒ n(U) = 50
Number of students who study French = 17
⇒ n(F) = 17
Number of students who study English = 13
⇒ n(E) = 13
Number of students who study Sanskrit = 15
⇒ n(S) = 15
Number of students who study French and English = 9
⇒ n(F ∩ E) = 9
Number of students who study English and Sanskrit = 4
⇒ n(E ∩ S) = 4
Number of students who study French and Sanskrit = 5
⇒ n(F ∩ S) = 5
Number of students who study French, English and Sanskrit = 3
⇒ n(F ∩ E ∩ S) = 3
n(F) = 17
a + b + d + e = 17 ......(i)
n(E) = 13
b + c + e + f = 13 ......(ii)
n(S) = 15
d + e + f + g = 15 ......(iii)
n(F ∩ E) = 9
∴ b + e = 9 ......(iv)
n(E ∩ S) = 4
∴ e + f = 4 .......(v)
n(F ∩ S) = 5
∴ d + e = 5 ......(vi)
n(E ∩ F ∩ S) = 3
∴ e = 3 .......(vii)
From (iv)
b + 3 = 9
⇒ b = 9 – 3 = 6
From (v)
3 + f = 4
⇒ f = 4 – 3 = 1
From (vi)
d + 3 = 5
⇒ d = 5 – 3 = 2
Now from equation (i)
a + 6 + 2 + 3 = 17
⇒ a = 17 – 11
⇒ a = 6
Now from equation (ii)
6 + c + 3 + 1 = 13
⇒ c = 13 – 10
⇒ c = 3
From equation (iii)
2 + 3 + 1 + g = 15
⇒ g = 15 – 6
⇒ g = 9
Number of students who study French and English but not Sanskrit, b = 6
APPEARS IN
संबंधित प्रश्न
Identify whether the following is set or not? Justify your answer.
The collection of ten most talented writers of India.
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
5 _____ A
Which of the following collection are sets? Justify your answer:
A collection of novels written by Munshi Prem Chand.
If A = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], then insert the appropriate symbol ∈ or ∉ in each of the following blank space:
12 ...... A
If A = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], then insert the appropriate symbol ∈ or ∉ in each of the following blank space:
9 ...... A
Describe the following sets in set-builder form:
B={1,1/2 ,1/3, 1/4,1/5,...........};
Describe the following sets in set-builder form:
{2, 4, 6, 8 .....}
List all the elements of the following set:
\[B = \left\{ x: x = \frac{1}{2n - 1}, 1 \leq n \leq 5 \right\}\]
Write the set of all positive integers whose cube is odd.
Write the set \[\left\{ \frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50} \right\}\] in the set-builder form.
Which of the following statement are correct?
Write a correct form of each of the incorrect statements.
\[a \subset \left\{ a, b, c \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ c, d \right\} \in A\]
Let A = {a, b, {c, d}, e}. Which of the following statements are false and why?
\[\left\{ a, b, e \right\} \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[2 \subset A\]
Write down all possible subsets of each of the following set:
{a, b, c},
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
2 _____ A
If A = {x/6x2 + x – 15 = 0}, B = {x/2x2 – 5x – 3 = 0}, C = {x/2x2 – x – 3 = 0} then find (A ∩ B ∩ C)
There are 260 persons with skin disorders. If 150 had been exposed to chemical A, 74 to chemical B, and 36 to both chemicals A and B, find the number of persons exposed to Chemical A but not Chemical B
Write the following interval in Set-Builder form
`(6, ∞)`
Write the following interval in Set-Builder form
(2, 5]
Write the following sets in the roaster form.
C = {x : x2 + 7x – 8 = 0, x ∈ R}
Let X = {1, 2, 3, 4, 5, 6}. If n represent any member of X, express the following as sets:
n is greater than 4
Write the following sets in the roaster from:
A = {x : x ∈ R, 2x + 11 = 15}
State which of the following statement is true and which is false. Justify your answer.
35 ∈ {x | x has exactly four positive factors}.
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in English and Mathematics but not in Science.
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English and Sanskrit but not French
In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is ______.
The set {x ∈ R : 1 ≤ x < 2} can be written as ______.
