Advertisements
Advertisements
प्रश्न
In Figure, ∠BAC = 90° and AD ⊥ BC. Then, ______.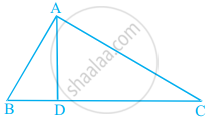
विकल्प
BD . CD = BC2
AB . AC = BC2
BD . CD = AD2
AB . AC = AD2
उत्तर
In Figure, ∠BAC = 90° and AD ⊥ BC. Then, BD . CD = AD2.
Explanation:

From ∆ADB and ∆ADC,
According to the question, we have,
∠D = ∠D = 90° ...(∵ AD ⊥ BC)
∠DBA = ∠DAC ...[Each angle = 90° – ∠C]
Using AAA similarity criteria,
∆ADB ∼ ∆ADC
`("BD")/("AD") = ("AD")/("CD")`
BD . CD = AD2
APPEARS IN
संबंधित प्रश्न
State whether the following quadrilaterals are similar or not:

Write the truth value (T/F) of each of the following statement
Any two congruent figures are similar.
For each of the following statements state whether true(T) or false (F)
any two rectangles are similar
For each of the following statements state whether true(T) or false (F)
if two triangles are similar then their corresponding angles are equal and their corresponding sides are equal
Similar triangles have the same ________ but not necessarily the same size
ΔPQR is an equilateral triangle with each side of length 2p. If PS ⊥ QR, then PS is equal to ______.
ΔABC is an equilateral A of side a. Its area will be ______.
In a rhombus if d1 = 16 cm, d2 = 12 cm, then the length of the side of the rhombus is ______.
If in two As ABC and DEF, `"AB"/"DF" = "BC"/"FE" = "CA"/"ED"`, then ______.
Observe the figures given below carefully and answer the questions:
| Figure A | 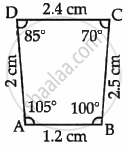 |
 |
| Figure B |  |
 |
| Figure C | 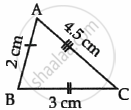 |
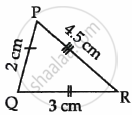 |
- Name the figure(s) where in two figures are similar.
- Name the figure(s) where in the figures are congruent.
-
- Prove that congruent triangles are also similar but not the converse.
OR - What more is least needed for two similar triangles to be congruent?
- Prove that congruent triangles are also similar but not the converse.
