Advertisements
Advertisements
प्रश्न
State whether the following quadrilaterals are similar or not:

उत्तर
Quadrilateral PQRS and ABCD are not similar as their corresponding sides are proportional, i.e. 1:2, but their corresponding angles are not equal.
APPEARS IN
संबंधित प्रश्न
Two polygons of the same number of sides are similar, if (a) their corresponding angles are ______ and (b) their corresponding sides are ______. (equal, proportional)
Two triangles are similar, if their corresponding angles are .......... (proportional, equal)
Two triangles are similar, if their corresponding sides are .......... (proportional, equal)
Write the truth value (T/F) of each of the following statement
Any two congruent figures are similar.
Write the truth value (T/F) of each of the following statement
Two polygons are similar if their corresponding angles are proportional.
For each of the following statements state whether true(T) or false (F)
Two circles with different radii are similar.
For each of the following statements state whether true(T) or false (F)
any two rectangles are similar
For each of the following statements state whether true(T) or false (F)
The length of the line segment joining the midpoints of any two sides of a triangles is equal to half the length of the third side.
For each of the following statements state whether true(T) or false (F)
the polygon formed by joining the midpoints of the sides of a quadrilateral is a rhombus.
For each of the following statements state whether true(T) or false (F)
the ratio of the perimeter of two similar triangles is the same as the ratio of the their corresponding medians.
If O is Any Point Inside a Rectangle Abcd Then `Oa^2+Oc^2=Ob^2+Od^2`
For each of the following statements state whether true(T) or false (F)
The sum of the squares on the sides of a rhombus is equal to the sum of the squares on its diagonals.
Similar triangles have the same ________ but not necessarily the same size
The symbol ~ is used to represent _________ triangles
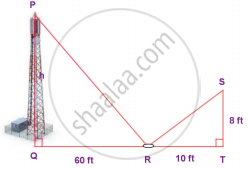
The height of a tower is measured by a mirror on the ground at R by which the top of the tower’s reflection is seen. Find the height of the tower. If ∆PQR ~ ∆STR
In Figure, ∠BAC = 90° and AD ⊥ BC. Then, ______.