Advertisements
Advertisements
प्रश्न
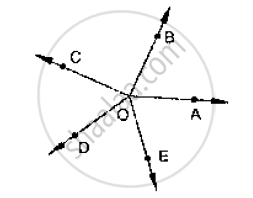
In the given below fig, rays OA, OB, OC, OP and 0E have the common end point O. Show
that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
उत्तर १
Given that
Rays OA, OB, OD and OE have the common end point O.
A ray of opposite to OA is drawn
Since `∠`AOB, `∠`BOF are linear pairs
`∠`AOB + `∠`BOF = 180°
`∠`AOB + `∠`BOC + `∠`COF = 180°
Also
`∠`AOE, `∠`EOF are linear pairs
`∠`AOE + `∠`EOF = 180°
`∠`AOE + `∠`DOF + `∠`DOE = 180°
By adding (1) and (2) quations we get
`∠`AOB + `∠`BOC + `∠`COF + `∠`AOE + `∠`DOF + `∠`DOE = 360°
`∠`AOB + `∠`BOC + `∠`COD + `∠`DOE + `∠`EOA = 360°
Hence proved.
उत्तर २
Let us draw AOXa straight line.
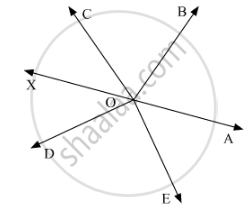
∠AOE,∠DOE and ∠DOXform a linear pair. Thus, their sum should be equal to180°.
Or, we can say that:
∠AOE +∠DOE +∠DOX = 180° (I)
Similarly,, ∠AOB,∠BOC and ∠COXform a linear pair. Thus, their sum should be equal to180°.
Or, we can say that:
∠AOB +∠BOC+ ∠COX = 180° (II)
On adding (I) and (II), we get:
∠AOB +∠BOC + ∠COX +∠DOX +∠AOE +∠DOE = 180°+180°
∠AOB +∠BOC + ∠COD +∠AOE +∠DOE = 360°
Hence proved.
APPEARS IN
संबंधित प्रश्न
If an angle is 28° less than its complement, find its measure.
In below fig, determine the value of x.

Fill in the blank so as to make the following statement true:
A ray stands on a line, then the sum of the two adjacent angles so formed is ______
If two straight lines intersect each other, prove that the ray opposite to the bisector of one of the angles thus formed bisects the vertically opposite angle.
The complement of an acute angle is ..............
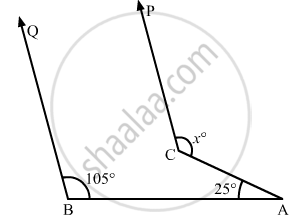
In the given figure, if CP || DQ, then the measure of x is
State, true or false:
An infinite number of straight lines can be drawn through a given point.
How many rays can be drawn through a fixed point O?
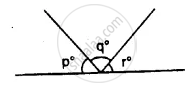
In the given figure. p° = q° = r°, find each.
Write the complement of `1/3` of 180°
