Advertisements
Advertisements
Question
In the given below fig, rays OA, OB, OC, OP and 0E have the common end point O. Show
that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
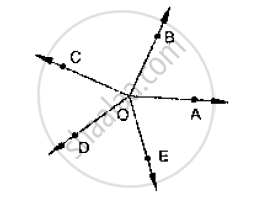
Solution 1
Given that
Rays OA, OB, OD and OE have the common end point O.
A ray of opposite to OA is drawn
Since `∠`AOB, `∠`BOF are linear pairs
`∠`AOB + `∠`BOF = 180°
`∠`AOB + `∠`BOC + `∠`COF = 180°
Also
`∠`AOE, `∠`EOF are linear pairs
`∠`AOE + `∠`EOF = 180°
`∠`AOE + `∠`DOF + `∠`DOE = 180°
By adding (1) and (2) quations we get
`∠`AOB + `∠`BOC + `∠`COF + `∠`AOE + `∠`DOF + `∠`DOE = 360°
`∠`AOB + `∠`BOC + `∠`COD + `∠`DOE + `∠`EOA = 360°
Hence proved.
Solution 2
Let us draw AOXa straight line.
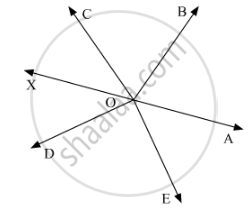
∠AOE,∠DOE and ∠DOXform a linear pair. Thus, their sum should be equal to180°.
Or, we can say that:
∠AOE +∠DOE +∠DOX = 180° (I)
Similarly,, ∠AOB,∠BOC and ∠COXform a linear pair. Thus, their sum should be equal to180°.
Or, we can say that:
∠AOB +∠BOC+ ∠COX = 180° (II)
On adding (I) and (II), we get:
∠AOB +∠BOC + ∠COX +∠DOX +∠AOE +∠DOE = 180°+180°
∠AOB +∠BOC + ∠COD +∠AOE +∠DOE = 360°
Hence proved.
APPEARS IN
RELATED QUESTIONS
If an angle is 30° more than one half of its complement, find the measure of the angle.
Write the complement of an angle of measure x°.
In the given figure, if l || m, what is the value of x?
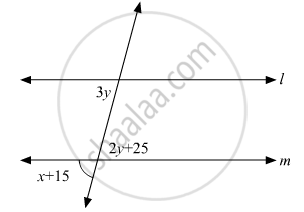
State, true or false:
A line segment 4 cm long can have only 2000 points in it.
In the following figure, ∠AOB and ∠AOC are adjacent angles? Give the reason for your answer.
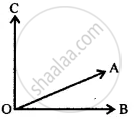
In the following figure, ∠AOB and ∠AOC are adjacent angles? Give the reason for your answer.
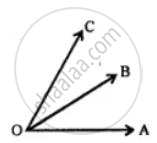
In the following figure, ∠AOB and ∠AOC are adjacent angles? Give the reason for your answer.
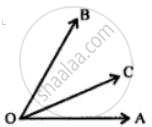
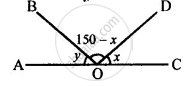
Find y in the given figure.
Write the complement of (x + 5)°
Write the supplement of x°
