Advertisements
Advertisements
प्रश्न
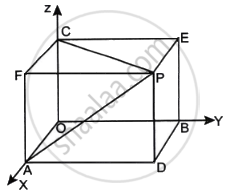
In the figure given below, if the coordinates of the point P are (a, b, c), then what are the perpendicular distances of P from XY, YZ and ZX planes respectively?
उत्तर
Coordinates of point P(a, b, c)
Then, x - coordinate of P is the perpendicular distance of P from the YZ plane
y - Coordinate of P is the perpendicular distance between P and the XZ plane
z - Coordinate of P is the perpendicular distance of P from the XZ plane.
Perpendicular distance from XY - plane = c
Perpendicular distance from YZ - plane = o
Perpendicular distance from XZ - plane = b
APPEARS IN
संबंधित प्रश्न
Find the equation of the planes parallel to the plane x + 2y+ 2z + 8 =0 which are at the distance of 2 units from the point (1,1, 2)
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x − y + z = 0. Also find the distance of the plane, obtained above, from the origin.
Write the equation of a plane which is at a distance of \[5\sqrt{3}\] units from origin and the normal to which is equally inclined to coordinate axes.
Find the distance of the point (2, 3, −5) from the plane x + 2y − 2z − 9 = 0.
Show that the points (1, 1, 1) and (−3, 0, 1) are equidistant from the plane 3x + 4y − 12z + 13 = 0.
Find the equations of the planes parallel to the plane x − 2y + 2z − 3 = 0 and which are at a unit distance from the point (1, 1, 1).
Find the distance of the point (3, 3, 3) from the plane \[\vec{r} \cdot \left( 5 \hat{i} + 2 \hat{j} - 7k \right) + 9 = 0\]
Find the distance between the point (7, 2, 4) and the plane determined by the points A(2, 5, −3), B(−2, −3, 5) and C (5, 3, −3).
The distance of the line \[\vec{r} = 2 \hat{i} - 2 \hat{j} + 3 \hat{k} + \lambda\left( \hat{i} - \hat{j}+ 4 \hat{k} \right)\] from the plane \[\vec{r} \cdot \left( \hat{i} + 5 \hat{j} + \hat{k} \right) = 5\] is
If a plane passes through the point (1, 1, 1) and is perpendicular to the line \[\frac{x - 1}{3} = \frac{y - 1}{0} = \frac{z - 1}{4}\] then its perpendicular distance from the origin is ______.
Find the distance of the point `4hat"i" - 3hat"j" + hat"k"` from the plane `bar"r".(2hat"i" + 3hat"j" - 6hat"k")` = 21.
Solve the following :
Find the distance of the point (13, 13, – 13) from the plane 3x + 4y – 12z = 0.
The perpendicular distance of the origin from the plane x − 3y + 4z = 6 is ______
The equation of the plane passing through (3, 1, 2) and making equal intercepts on the coordinate axes is _______.
Find the distance of the point whose position vector is `(2hat"i" + hat"j" - hat"k")` from the plane `vec"r" * (hat"i" - 2hat"j" + 4hat"k")` = 9
A plane meets the co-ordinates axis in A, B, C such that the centroid of the ∆ABC is the point (α, β, γ). Show that the equation of the plane is `x/alpha + y/beta + z/ϒ` = 3
Find the distance of a point (2, 4, –1) from the line `(x + 5)/1 = (y + 3)/4 = (z - 6)/(-9)`
Which one of the following statements is correct for a moving body?
A metro train starts from rest and in 5 s achieves 108 km/h. After that it moves with constant velocity and comes to rest after travelling 45 m with uniform retardation. If total distance travelled is 395 m, find total time of travelling.
The coordinates of the point on the parabola y2 = 8x which is at minimum distance from the circle x2 + (y + 6)2 = 1 are
If the distance of the point (1, 1, 1) from the plane x – y + z + λ = 0 is `5/sqrt(3)`, find the value(s) of λ.
Find the distance of the point (1, –2, 0) from the point of the line `vecr = 4hati + 2hatj + 7hatk + λ(3hati + 4hatj + 2hatk)` and the point `vecr.(hati - hatj + hatk)` = 10.
Find the coordinates of points on line `x/1 = (y - 1)/2 = (z + 1)/2` which are at a distance of `sqrt(11)` units from origin.
The distance of the point `2hati + hatj - hatk` from the plane `vecr.(hati - 2hatj + 4hatk)` = 9 will be ______.
