Advertisements
Advertisements
प्रश्न
In the figure, PQRS is cyclic, side PQ ≅ side RQ, ∠PSR = 110°. Find
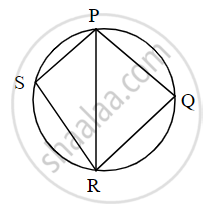
(i) measure of ∠PQR
(ii) m(arc PQR)
(iii) m(arc QR)
उत्तर
(i) ▢PQRS is a cyclic quadrilateral. ...[Given]
∴ ∠PSR + ∠PQR = 180° ...[Opposite angles of a cyclic quadrilateral are supplementary]
∴ 110° + ∠PQR = 180°
∴ ∠PQR = 180° − 110°
∴ m∠PQR = 70°
(ii) ∠PSR = `1/2` m(arc PQR) .....[Inscribed angle theorem]
∴ 110° = `1/2` m(arc PQR)
∴ m(arc PQR) = 220°
(iii) In ∆PQR,
Side PQ ≅ side RQ ...[Given]
∴ ∠PRQ ≅ ∠QPR ...[Isosceles triangle theorem]
Let ∠PRQ = ∠QPR = x
Now, ∠PQR + ∠QPR + ∠PRQ = 180° ...[Sum of the measures of angles of a triangle is 180°]
∴ ∠PQR + x + x = 180°
∴ 70° + 2x = 180°
∴ 2x = 180° − 70°
∴ 2x = 110°
∴ x = `110^circ/2`
∴ x = 55°
∴ ∠PRQ = ∠QPR = 55° ......(i)
But, ∠QPR = `1/2` m(arc QR) .....[Inscribed angle theorem]
∴ 55° = `1/2` m(arc QR)
∴ m(arc QR) = 110°
APPEARS IN
संबंधित प्रश्न
Prove that the “the opposite angles of the cyclic quadrilateral are supplementary”.
Prove that “The opposite angles of a cyclic quadrilateral are supplementary”.
In the given figure, ▢PQRS is cyclic. side PQ ≅ side RQ. ∠PSR = 110°, Find -
(1) measure of ∠PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠PRQ

`square`MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N.
Prove that, any rectangle is a cyclic quadrilateral
In the given figure, line PR touches the circle at point Q. Answer the following questions with the help of the figure.
(1) What is the sum of ∠ TAQ and ∠ TSQ ?
(2) Find the angles which are congruent to ∠ AQP.
(3) Which angles are congruent to ∠ QTS ?
(4) ∠TAS = 65°, find the measure of ∠TQS and arc TS.
(5) If ∠AQP = 42°and ∠SQR = 58° find measure of ∠ATS.

In the given figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q respectively. Prove that : seg SQ || seg RP.

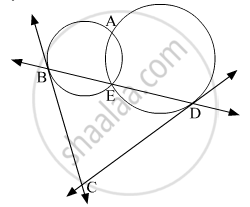
In the given figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that ▢ABCD is cyclic.
In the given figure, seg AD ⊥ side BC, seg BE ⊥ side AC, seg CF ⊥ side AB. Ponit O is the orthocentre. Prove that , point O is the incentre of ∆DEF.

Find the value of x in the given figure.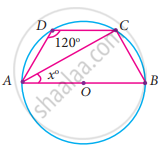
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6 m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8 m, CD = 10 m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.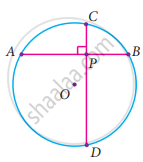
MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N, by completing the following activity.
Solution:
MRPN is cyclic
The opposite angles of a cyclic square are `square`
∠R + ∠N = `square`
∴ (5x – 13)° + (4x + 4)° = `square`
∴ 9x = 189°
∴ x = `square`
∴ ∠R = (5x – 13)° = `square`
∴ ∠N = (4x + 4)° = `square`
Prove the following theorems:
Opposite angles of a cyclic quadrilateral are supplementary.
If two consecutive angles of cyclic quadrilateral are congruent, then prove that one pair of opposite sides is congruent and other is parallel.
