Advertisements
Advertisements
प्रश्न
In the given figure, seg AD ⊥ side BC, seg BE ⊥ side AC, seg CF ⊥ side AB. Ponit O is the orthocentre. Prove that , point O is the incentre of ∆DEF.

उत्तर
It is given that seg AD ⊥ side BC, seg BE ⊥ side AC and seg CF ⊥ side BC. O is the orthocentre of ∆ABC.
Join DE, EF and DF.
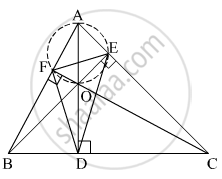
∠AFO + ∠AEO = 90º + 90º = 180º
∴ Quadrilateral AEOF is cyclic. (If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic)
⇒ ∠OAE = ∠OFE .....(1) (Angles inscribed in the same arc are congruent)
∠BFO + ∠BDO = 90º + 90º = 180º
∴ Quadrilateral BFOD is cyclic. (If a pair of opposite angles of a quadrilateral is supplementary, the quadrilateral is cyclic)
∴ seg OD subtends equal angles ∠OFD and ∠OBD on the same side of OD.
⇒ ∠OBD = ∠OFD .....(2) (Angles inscribed in the same arc are congruent)
In ∆ACD,
∠DAC + ∠ACD = 90º .....(3) (Using angle sum property of triangle)
In ∆BCE,
∠BCE + ∠CBE = 90º .....(4) (Using angle sum property of triangle)
From (3) and (4), we get
∠DAC + ∠ACD = ∠BCE + ∠CBE
⇒ ∠DAC = ∠CBE .....(5)
From (1), (2) and (5), we get
∠OFE = ∠OFD
⇒ OF is the bisector of ∠EFD.
Similarly, OE and OD are the bisectors of ∠DEF and ∠EDF, respectively.
Hence, O is the incentre of ∆DEF. (Incentre of a triangle is the point of intersection of its angle bisectors)
APPEARS IN
संबंधित प्रश्न
Prove that the “the opposite angles of the cyclic quadrilateral are supplementary”.
Prove that “The opposite angles of a cyclic quadrilateral are supplementary”.
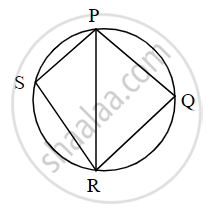
In the given figure, ▢PQRS is cyclic. side PQ ≅ side RQ. ∠PSR = 110°, Find -
(1) measure of ∠PQR
(2) m(arc PQR)
(3) m(arc QR)
(4) measure of ∠PRQ
`square`MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N.
Prove that, any rectangle is a cyclic quadrilateral
In the given figure, line PR touches the circle at point Q. Answer the following questions with the help of the figure.
(1) What is the sum of ∠ TAQ and ∠ TSQ ?
(2) Find the angles which are congruent to ∠ AQP.
(3) Which angles are congruent to ∠ QTS ?
(4) ∠TAS = 65°, find the measure of ∠TQS and arc TS.
(5) If ∠AQP = 42°and ∠SQR = 58° find measure of ∠ATS.

In the given figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R, S and P, Q respectively. Prove that : seg SQ || seg RP.

Find the value of x in the given figure.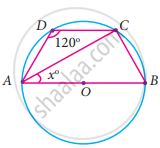
A school wants to conduct tree plantation programme. For this a teacher allotted a circle of radius 6 m ground to nineth standard students for planting sapplings. Four students plant trees at the points A, B, C and D as shown in figure. Here AB = 8 m, CD = 10 m and AB ⊥ CD. If another student places a flower pot at the point P, the intersection of AB and CD, then find the distance from the centre to P.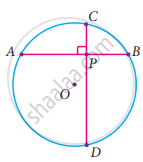
MRPN is cyclic, ∠R = (5x – 13)°, ∠N = (4x + 4)°. Find measures of ∠R and ∠N, by completing the following activity.
Solution:
MRPN is cyclic
The opposite angles of a cyclic square are `square`
∠R + ∠N = `square`
∴ (5x – 13)° + (4x + 4)° = `square`
∴ 9x = 189°
∴ x = `square`
∴ ∠R = (5x – 13)° = `square`
∴ ∠N = (4x + 4)° = `square`
Prove the following theorems:
Opposite angles of a cyclic quadrilateral are supplementary.
In the figure, PQRS is cyclic, side PQ ≅ side RQ, ∠PSR = 110°. Find

(i) measure of ∠PQR
(ii) m(arc PQR)
(iii) m(arc QR)
