Advertisements
Advertisements
प्रश्न
In the given figure, an equilateral triangle ABC is inscribed in a circle with center O.
Find: (i) ∠BOC
(ii) ∠OBC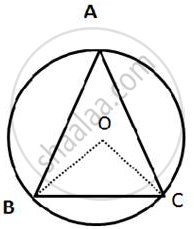
उत्तर
In the given figure, ABC is an equilateral triangle.
Hence all the three angles of the triangle will be equal to 60°
i.e. ∠A = ∠B = ∠C = 60°
As the triangle is an equilateral triangle, BO and CO will be the angle bisectors of B and C respectively.
Hence ∠OBC = `"∠ABC"/2`
= 30°
and as given in the figure we can see that OB and OC are the radii of the given circle.
Hence they are of equal length.
The ΔOBC is an isosceles triangle with OB = OC
In ΔOBC,
∠OBC = ∠OCB as they are angles opposite to the two equal sides of an isosceles triangle.
Hence, ∠OBC = 30° and ∠OCB = 30°
Since the sum of all angles of a triangle is 180°
Hence in triangle OBC, ∠OCB + ∠OBC + ∠BOC + BOC = 180°
30° + 30° + ∠BOC= 180°
60° + BOC = 180°
∠BOC = 180° - 60°
∠BOC = 120°
Hence ∠BOC =120° and ∠OBC =30°
APPEARS IN
संबंधित प्रश्न
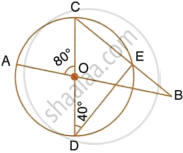
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in:
- ∠DCE,
- ∠ABC.
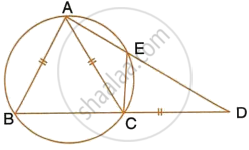
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate :
- Angle ABC
- Angle BEC
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
- angle QTR
- angle QRP
- angle QRS
- angle STR
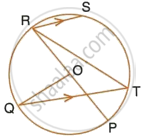
The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(ii) angle QRP

The given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT = 20° and angle POQ = 100°. Calculate:
(iv) angle STR

In the given figure, O is the center of the circle and the length of arc AB is twice the length of arc BC. If ∠AOB = 100°,
find: (i) ∠BOC (ii) ∠OAC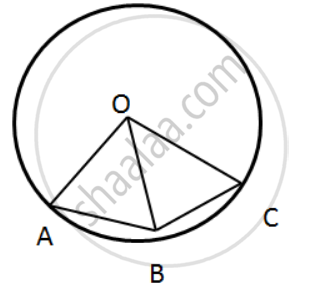
In the given figure, AB is a side of a regular hexagon and AC is a side of a regular eight-sided polygon.
Find:
(i) ∠AOB
(ii) ∠AOC
(iii) ∠BOC
(iv) ∠OBC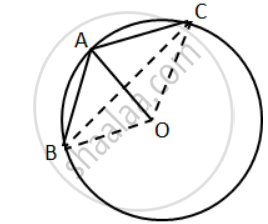
In the given figure, AB = BC = DC and ∠AOB = 50°.
(i) ∠AOC
(ii) ∠AOD
(iii) ∠BOD
(iv) ∠OAC
(v) ∠ODA
In the given figure, arc AB and arc BC are equal in length. If ∠AOB = 48°, find:
(i) ∠BOC
(ii) ∠OBC
(iii) ∠AOC
(iv) ∠OAC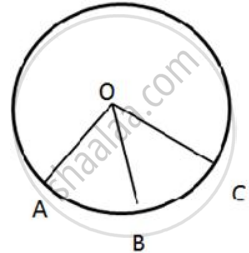
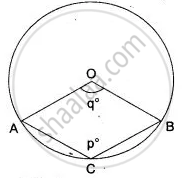
C is a point on the minor arc AB of the circle, with centre O. Given ∠ACB = p°, ∠AOB = q°.
(i) Express q in terms of p.
(ii) Calculate p if ACBO is a parallelogram.
(iii) If ACBO is a parallelogram, then find the value of q + p.