Advertisements
Advertisements
प्रश्न
In the given figure, BAC is a straight line.
Find:
(i) x
(ii) ∠AOB
(iii) ∠BOC

उत्तर
∵ ∠AOB and ∠COB are linear pairs
∴ ∠AOB + ∠COB = 180°
⇒ x + 25° + 3x + 15° = 180°
⇒ 4x + 40° = 180°
⇒ 4x = 180°− 40° = 140°
(i) ⇒ x =`(140°)/4=35°`
Hence, x = 35°
(ii) ∠AOB = x + 25° = 35° + 25° = 60°
(iii) ∠BOC = 3x + 15° = 3 × 35° + 15°
= 105° + 15° = 120°
APPEARS IN
संबंधित प्रश्न
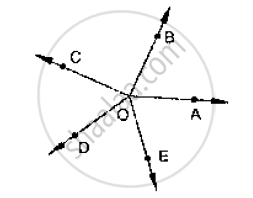
In the given below fig, rays OA, OB, OC, OP and 0E have the common end point O. Show
that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
In below fig, determine the value of x.

In the below fig, POQ is a line. Ray OR is perpendicular to line OS is another ray lying
between rays OP and OR. Prove that ∠ROS = 1 (∠QOS − ∠POS).

The supplement of an acute angle is .................
Write the supplement of an angle of measure 2y°.
If a wheel has six spokes equally spaced, then find the measure of the angle between two adjacent spokes.
Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC =
State, true or false:
A line segment 4 cm long can have only 2000 points in it.
State, true or false:
An infinite number of straight lines can be drawn through a given point.
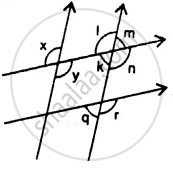
In the given figure, the arrows indicate parallel lines. State which angles are equal. Give a reason.