Advertisements
Advertisements
Question
In the given figure, BAC is a straight line.
Find:
(i) x
(ii) ∠AOB
(iii) ∠BOC

Solution
∵ ∠AOB and ∠COB are linear pairs
∴ ∠AOB + ∠COB = 180°
⇒ x + 25° + 3x + 15° = 180°
⇒ 4x + 40° = 180°
⇒ 4x = 180°− 40° = 140°
(i) ⇒ x =`(140°)/4=35°`
Hence, x = 35°
(ii) ∠AOB = x + 25° = 35° + 25° = 60°
(iii) ∠BOC = 3x + 15° = 3 × 35° + 15°
= 105° + 15° = 120°
APPEARS IN
RELATED QUESTIONS
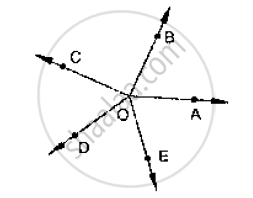
In the given below fig, rays OA, OB, OC, OP and 0E have the common end point O. Show
that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
Define complementary angles.
An angle is equal to five times its complement. Determine its measure.
Two complementary angles are such that two times the measure of one is equal to three times the measure of the other. The measure of the smaller angle is
State, true or false:
A line segment 4 cm long can have only 2000 points in it.
State, true or false:
An infinite number of straight lines can be drawn through a given point.
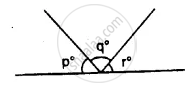
In the given figure. p° = q° = r°, find each.
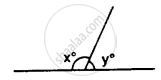
In the given figure, if x = 2y, find x and y
Write the complement of `1/2` of a right angle
Write the supplement of 0°
