Question

In two concentric circles, a chord of length 24 cm of larger circle touches the smaller circle, whose radius is 5 cm. Find the radius of the larger circle.

Answer 1

Given:

OX = 5 cm

AB = 24 cm

To find: OA (Radius of Larger Circle)

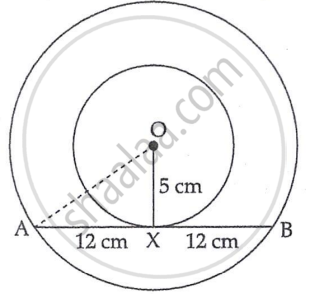
OX ⊥ AB (∵ Radius drawn from the centre of a circle is ⊥ to the Chord)   ...(i)

And, X is mid point of AB

(∵ Perpendicular drawn from the centre of a circle to the chord bisects the chord)   ...(ii)

From (i) and (ii)

ΔOAX is a right angled triangle

∠OXA = 90°

AX = 12 cm

By Using Pythagoras theorem.

OA² = OX² + AX²

= 5² + 12²

= 25 + 144

= 169

OA = 13 cm.