Advertisements
Advertisements
प्रश्न
In what ratio does the y-axis divides the line joining the points (−5, 1) and (2, 3) internally
विकल्प
1 : 3
2 : 5
3 : 1
5 : 2
उत्तर
5 : 2
Explanation;
Hint:
When it cut the y-axis the point P is (0, a)
A line divides internally in the ratio m : n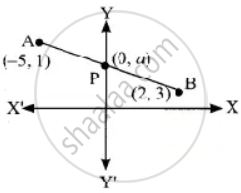
The point P = `(("m"x_2 + "n"x_1)/("m" + "n"), ("m"y_2 + "n"y_1)/("m" + "n"))`
(0, a) = `((2"m" - 5"n")/("m" + "n"), (3"m" + "n")/("m" + "n"))`
`(2"m" - 5"n")/("m" + "n")` = 0
2m – 5n = 0
⇒ 2m = 5n
`"m"/"n" = 5/2`
⇒ m : n = 5 : 2
APPEARS IN
संबंधित प्रश्न
Write the co-ordinates of the point of intersection of graphs of
equations x = 2 and y = -3.
Complete the table below the graph with the help of the following graph.

| Sr. No. | First point | Second point | Co-ordinates of first point (x1 , y1) | Co-ordinates of second point (x2 , y2) | `(y_2 - y_2)/(x_2 - x_2)` |
| 1 | C | E | (1, 0) | (3,4) | `4/2=2` |
| 2 | A | B | (-1,-4) | (0,-2) | `2/1 = 2` |
| 3 | B | D | (0,-2) | (2,2) | `4/2=2` |
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
A triangle is formed by line segments joining the points (5, 1 ), (3, 4) and (1, 1). Find the coordinates of the centroid.
The mid point of the line segment joining the points (p, 2) and (3, 6) is (2, q). Find the numerical values of a and b.
The three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
If `"P"("a"/3, "b"/2)` is the mid-point of the line segment joining A(−4, 3) and B(−2, 4) then (a, b) is
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
Find the coordinates of the mid-point of the line segment with points A(– 2, 4) and B(–6, –6) on both ends.
