Advertisements
Advertisements
प्रश्न
The mid-point of the line joining (−a, 2b) and (−3a, −4b) is
विकल्प
(2a, 3b)
(−2a, −b)
(2a, b)
(−2a, −3b)
उत्तर
(−2a, −b)
Explanation;
Hint:
Mid−points of line = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
= `((-"a" - 3"a")/2, (2"b" - 4"b")/2)`
= `((-4"a")/2, (-2"b")/2)`
= (−2a, −b)
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, -4). Find
1) Coordinates of A
2) An equation of diagonal BD
Given M is the mid-point of AB, find the co-ordinates of B; if A = (3, –1) and M = (–1, 3).
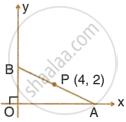
In the given figure, P(4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
A(–1, 0), B(1, 3) and D(3, 5) are the vertices of a parallelogram ABCD. Find the co-ordinates of vertex C.
Calculate the co-ordinates of the centroid of the triangle ABC, if A = (7, –2), B = (0, 1) and C =(–1, 4).
If the midpoints of the sides ofa triangle are (-2, 3), (4, -3), (4, 5), find its vertices.
Find coordinates of midpoint of segment joining (– 2, 6) and (8, 2)
If A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ∆ABC. Segment AD is median. Find the length of seg AD:
If the vertices of a triangle are (1, 3), (2, - 4) and (-3, 1). Then the co-ordinate of its centroid is:
Find the co-ordinates of centroid of a triangle if points D(–7, 6), E(8, 5) and F(2, –2) are the mid-points of the sides of that triangle.
