Advertisements
Advertisements
प्रश्न
The mid-point of the line joining (−a, 2b) and (−3a, −4b) is
पर्याय
(2a, 3b)
(−2a, −b)
(2a, b)
(−2a, −3b)
उत्तर
(−2a, −b)
Explanation;
Hint:
Mid−points of line = `((x_1 + x_2)/2, (y_1 + y_2)/2)`
= `((-"a" - 3"a")/2, (2"b" - 4"b")/2)`
= `((-4"a")/2, (-2"b")/2)`
= (−2a, −b)
APPEARS IN
संबंधित प्रश्न
Points P(a, −4), Q(−2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.
Three consecutive vertices of a parallelogram ABCD are A(S, 5), B(-7, -5) and C(-5, 5). Find the coordinates of the fourth vertex D.
Find the centroid of a triangle whose vertices are (3, -5), (-7, 4) and ( 10, -2).
P , Q and R are collinear points such that PQ = QR . IF the coordinates of P , Q and R are (-5 , x) , (y , 7) , (1 , -3) respectively, find the values of x and y.
AB is a diameter of a circle with centre 0. If the ooordinates of A and 0 are ( 1, 4) and (3, 6 ). Find the ooordinates of B and the length of the diameter.
Find the mid-point of the line segment joining the points
(−2, 3) and (−6, −5)
Find the mid-point of the line segment joining the points
(8, −2) and (−8, 0)
The points A(−3, 6), B(0, 7) and C(1, 9) are the mid-points of the sides DE, EF and FD of a triangle DEF. Show that the quadrilateral ABCD is a parallelogram.
The coordinates of the point C dividing the line segment joining the points P(2, 4) and Q(5, 7) internally in the ratio 2 : 1 is
Point P is the centre of the circle and AB is a diameter. Find the coordinates of points B if coordinates of point A and P are (2, – 3) and (– 2, 0) respectively.
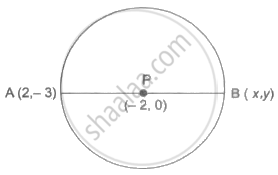
Given: A`square` and P`square`. Let B (x, y)
The centre of the circle is the midpoint of the diameter.
∴ Mid point formula,
`square = (square + x)/square`
⇒ `square = square` + x
⇒ x = `square - square`
⇒ x = – 6
and `square = (square + y)/2`
⇒ `square` + y = 0
⇒ y = 3
Hence coordinates of B is (– 6, 3).
