Advertisements
Advertisements
प्रश्न
It is found that yellow light does not eject photoelectrons from a metal. Is it advisable to try with orange light or with green light?
उत्तर
Photoelectrons are emitted from a metal's surface if the frequency of incident radiation is more than the threshold frequency of the given metal surface. As yellow light does not eject photoelectrons from a metal it means that the threshold frequency of the metal is more than the frequency of yellow light. Since the frequency of orange light is less than the frequency of yellow light, therefore it will not be able to eject photoelectrons from the metal's surface. The frequency of green light is more than the frequency of yellow light. Hence, when it is incident on the metal surface, it will eject electrons from the metal.
APPEARS IN
संबंधित प्रश्न
(a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter. Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its e/m is given to be 1.76 × 1011 C kg−1.
(b) Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. Do you see what is wrong? In what way is the formula to be modified?
Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. Do you see what is wrong? In what way is the formula to be modified?
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1 = 3650 Å, λ2 = 4047 Å, λ3 = 4358 Å, λ4 = 5461 Å, λ5 = 6907 Å,
The stopping voltages, respectively, were measured to be:
V01 = 1.28 V, V02 = 0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 × 10−19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
Light of intensity 10−5 W m−2 falls on a sodium photo-cell of surface area 2 cm2. Assuming that the top 5 layers of sodium absorb the incident energy, estimate time required for photoelectric emission in the wave-picture of radiation. The work function for the metal is given to be about 2 eV. What is the implication of your answer?
Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?
It is found that photosynthesis starts in certain plants when exposed to sunlight, but it does not start if the plants are exposed only to infrared light. Explain.
Planck's constant has the same dimensions as
When stopping potential is applied in an experiment on photoelectric effect, no photoelectric is observed. This means that
Calculate the momentum of a photon of light of wavelength 500 nm.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflecting plane mirror. The angle of incidence is 60° and the number of photons striking the mirror per second is 1.0 × 1019. Calculate the force exerted by the light beam on the mirror.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
The work function of a photoelectric material is 4.0 eV. (a) What is the threshold wavelength? (b) Find the wavelength of light for which the stopping potential is 2.5 V.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
When a metal plate is exposed to a monochromatic beam of light of wavelength 400 nm, a negative potential of 1.1 V is needed to stop the photo current. Find the threshold wavelength for the metal.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In the case of photoelectric effect experiment, explain the following facts, giving reasons.
The photoelectric current increases with increase of intensity of incident light.
Explain how does (i) photoelectric current and (ii) kinetic energy of the photoelectrons emitted in a photocell vary if the frequency of incident radiation is doubled, but keeping the intensity same?
Show the graphical variation in the above two cases.
Consider a 20 W bulb emitting light of wavelength 5000 Å and shining on a metal surface kept at a distance 2 m. Assume that the metal surface has work function of 2 eV and that each atom on the metal surface can be treated as a circular disk of radius 1.5 Å.
- Estimate no. of photons emitted by the bulb per second. [Assume no other losses]
- Will there be photoelectric emission?
- How much time would be required by the atomic disk to receive energy equal to work function (2 eV)?
- How many photons would atomic disk receive within time duration calculated in (iii) above?
- Can you explain how photoelectric effect was observed instantaneously?
The graph shows the variation of photocurrent for a photosensitive metal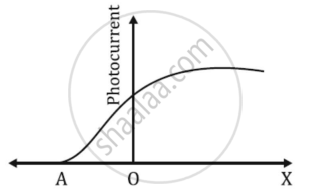
- What does X and A on the horizontal axis represent?
- Draw this graph for three different values of frequencies of incident radiation ʋ1, ʋ2 and ʋ3 (ʋ3 > ʋ2 > ʋ1) for the same intensity.
- Draw this graph for three different values of intensities of incident radiation I1, I2 and I3 (I3 > I2 > I1) having the same frequency.
How would the stopping potential for a given photosensitive surface change if the frequency of the incident radiation were increased? Justify your answer.
