Advertisements
Advertisements
प्रश्न
When a metal plate is exposed to a monochromatic beam of light of wavelength 400 nm, a negative potential of 1.1 V is needed to stop the photo current. Find the threshold wavelength for the metal.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
उत्तर
Given :-
Wavelength of light, `λ = 400 "nm" = 400 xx 10^-9 "m"`
Stopping potential, `V_0 = 1.1 V`
From Einstein's photoelectric equation,
`(hc)/λ = (hc)/(λ_0) + eV_0`,
where h = Planck's constant
c = speed of light
λ = wavelength of light
`λ_0` = threshold wavelength
`V_0` = stopping potential
On substituting the respective values in the above formula , we get :
`(6.63 xx 10^-34 xx 3 xx 10^8)/(400 xx 10^-9) = (6.63 xx 10^-34 xx 3 xx 10^8)/λ_0 + 1.6 xx 10^-19 xx 1.1`
`⇒ 4.97 xx 10^-19 = (19.89 xx 10^-26)/λ_0 + 1.76 xx 10^-19`
`⇒ 4.97 = (19.89 xx 10^-7)/λ_0 + 1.76`
`⇒ (19.89 xx 10^-7)/λ_0 = 4.97 - 1.76 = 3.21`
`⇒ λ_0 = (19.89 xx 10^-7)/3.21`
`= 6.196 xx 10^-7 "m" = 620 "nm"`
APPEARS IN
संबंधित प्रश्न
The photoelectric cut-off voltage in a certain experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons emitted?
Ultraviolet light of wavelength 2271 Å from a 100 W mercury source irradiates a photo-cell made of molybdenum metal. If the stopping potential is −1.3 V, estimate the work function of the metal. How would the photo-cell respond to a high intensity (∼105 W m−2) red light of wavelength 6328 Å produced by a He-Ne laser?
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1 = 3650 Å, λ2 = 4047 Å, λ3 = 4358 Å, λ4 = 5461 Å, λ5 = 6907 Å,
The stopping voltages, respectively, were measured to be:
V01 = 1.28 V, V02 = 0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 × 10−19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
Light of intensity 10−5 W m−2 falls on a sodium photo-cell of surface area 2 cm2. Assuming that the top 5 layers of sodium absorb the incident energy, estimate time required for photoelectric emission in the wave-picture of radiation. The work function for the metal is given to be about 2 eV. What is the implication of your answer?
Two photons of
The equation E = pc is valid
The work function of a metal is hv0. Light of frequency v falls on this metal. Photoelectric effect will take place only if
When the intensity of a light source in increased,
(a) the number of photons emitted by the source in unit time increases
(b) the total energy of the photons emitted per unit time increases
(c) more energetic photons are emitted
(d) faster photons are emitted
Photoelectric effect supports quantum nature of light because
(a) there is a minimum frequency below which no photoelectrons are emitted
(b) the maximum kinetic energy of photoelectrons depends only on the frequency of light and not on its intensity
(c) even when the metal surface is faintly illuminated the photoelectrons leave the surface immediately
(d) electric charge of the photoelectrons is quantised
An atom absorbs a photon of wavelength 500 nm and emits another photon of wavelength 700 nm. Find the net energy absorbed by the atom in the process.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflecting plane mirror. The angle of incidence is 60° and the number of photons striking the mirror per second is 1.0 × 1019. Calculate the force exerted by the light beam on the mirror.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Show that it is not possible for a photon to be completely absorbed by a free electron.
Find the maximum kinetic energy of the photoelectrons ejected when light of wavelength 350 nm is incident on a cesium surface. Work function of cesium = 1.9 eV
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
The electric field associated with a monochromatic beam is 1.2 × 1015 times per second. Find the maximum kinetic energy of the photoelectrons when this light falls on a metal surface whose work function is 2.0 eV.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
The figure is the plot of stopping potential versus the frequency of the light used in an experiment on photoelectric effect. Find (a) the ratio h/e and (b) the work function.
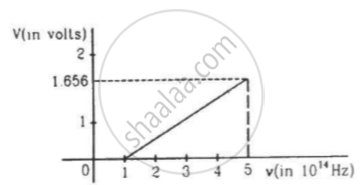
In photoelectric effect the photo current ______.
Consider a metal exposed to light of wavelength 600 nm. The maximum energy of the electron doubles when light of wavelength 400 nm is used. Find the work function in eV.
Consider a thin target (10–2 cm square, 10–3 m thickness) of sodium, which produces a photocurrent of 100 µA when a light of intensity 100W/m2 (λ = 660 nm) falls on it. Find the probability that a photoelectron is produced when a photons strikes a sodium atom. [Take density of Na = 0.97 kg/m3].
The figure shows a plot of stopping potential (V0) versus `1/lambda`, where λ is the wavelength of the radiation causing photoelectric emission from a surface. The slope of the line is equal to ______.
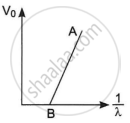
A metallic plate exposed to white light emits electrons. For which of the following colours of light, the stopping potential will be maximum?
