Advertisements
Advertisements
प्रश्न
किसी त्रिभुज PQR की भुजाओं PQ और PR पर क्रमश : बिंद A और B इस प्रकार स्थित हैं कि PQ = 12.5 cm, PA = 5 cm, BR = 6 cm और PB = 4 cm हैं। क्या AB || QR है? अपने उत्तर के लिए कारण दीजिए।
उत्तर
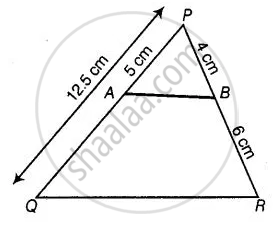
दिया गया है,
PQ = 12.5 cm,
PA = 5 cm,
BR = 6 cm
और PB = 4 cm
फिर, QA = QP – PA
= 12.5 – 5
= 7.5 cm
अब, `("PA")/("AQ")`
= `5/7.5`
= `50/75`
= `2/3` ...(i)
और `("PB")/("BR")`
= `4/6`
= `2/3` ...(ii)
समीकरण (i) और (ii) से,
`("PA")/("AQ") = ("PB")/("BR")`
आधारभूत समानुपातिक प्रमेय के विलोम से,
AB || QR
APPEARS IN
संबंधित प्रश्न
आकृति में, DE || BC है। AD ज्ञात कीजिए:
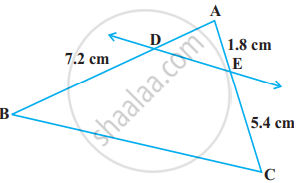
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
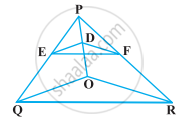
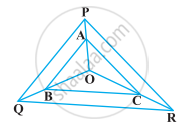
आकृति में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
ABCD एक समलंब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि `"AO"/"BO" = "CO"/"DO"` है।
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
यह दिया है कि `(BC)/(QR) = 1/3` के साथ ΔABC ~ ΔPQR, है। तब `(ar(PRQ))/(ar(BCA))` बराबर ______ है।
ΔDEF ~ ΔRPQ दिया है। क्या कहना सत्य है कि ∠D = ∠R और ∠F = ∠P? क्यों?
सिद्ध कीजिए कि समबाहु त्रिभुज के सभी कोण न्यून कोण होते हैं।
