Question

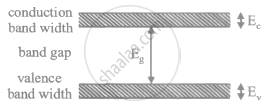
Let ΔE denote the energy gap between the valence band and the conduction band. The population of conduction electrons (and of the holes) is roughly proportional to e^−ΔE/2kT. Find the ratio of the concentration of conduction electrons in diamond to the in silicon at room temperature 300 K. ΔE for silicon is 1.1 eV and for diamond is 6.1 eV. How many conduction electrons are likely to be in one cubic metre of diamond?

Answer 1

Given:
Number of electrons in the conduction band, n = e^−ΔE/2kT
Band gap of diamond, ΔE₁ = 6 eV
Band gap of silicon, ΔE₂ = 1.1 eV
Now,

\[n_{\text{ diamond}}  =  e^\frac{- \Delta E_1}{2\text{ kT}} \] 

\[ n_{\text{ silicon}}  =  e^\frac{- \Delta E_2}{2\text{ kT}} \] 

\[ \therefore \frac{n_{\text{ diamond }}}{n_{\text{ silicon}}} =  e^\frac{- 1}{2kT}( ∆ E_1 - ∆ E_2 ) \] 

\[ \Rightarrow \frac{n_{\text{diamond}}}{n_{\text{silicon}}} =  e^\frac{- 1}{2 \times 8 . 62 \times {10}^{- 5} \times 300}(6 . 0 - 1 . 1) \] 

\[ \Rightarrow \frac{n_{\text{diamond}}}{n_{\text{silicon}}} = 7 . 15 \times  {10}^{- 42}\]

Because of more band gap, the conduction electrons per cubic metre in diamond are very less as compared to those in silicon, or we can simply say that they are almost zero.