Advertisements
Advertisements
प्रश्न
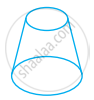
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
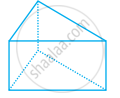
उत्तर
In the given figure, we have
Faces (F) = 5, Vertices (V) = 6 and Edges (E) = 9
On putting these values in Euler's formula, we get
F + V – E = 2
⇒ 5 + 6 – 9 = 2
⇒ 11 – 9 = 2
⇒ 2 = 2
Hence, these values satisfies the Euler's formula. So, it is a polyhedra.
APPEARS IN
संबंधित प्रश्न
Using Euler’s formula, find V if E = 30, F = 12.
Verify Euler’s formula for the following three-dimensional figures:

If a solid shape has 12 faces and 20 vertices, then the number of edges in this solid is ______.
Complete the table given below:
| S.No | Solid | Shape of Solid |
Number of faces F |
Number of Verticles V |
Number of edges E |
F + V | E + 2 |
| a. | Cuboid |  |
|||||
| b. | Triangular Pyramid |
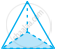 |
|||||
| c. | Square Pyramid |
 |
|||||
| d. | Rectangular Pyramid |
 |
|||||
| e. | Pentagonal Pyramid |
 |
|||||
| f. | Hexagonal Pyramid |
 |
|||||
| g. | Triangular Prism |
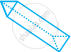 |
|||||
| h. | Square Prism |
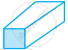 |
|||||
| i. | Cube |  |
|||||
| j. | Pentagonal Prism |
 |
|||||
| k. | Octagonal Prism |
 |
|||||
| l. | Heptagonal Prism |
 |
Look at the shapes given below and state which of these are polyhedra using Euler’s formula.
Using Euler’s formula, find the value of unknown y in the following table.
| Faces | y |
| Vertices | 12 |
| Edges | 18 |
Using Euler’s formula, find the value of unknown p in the following table.
| Faces | p |
| Vertices | 6 |
| Edges | 12 |
Using Euler’s formula, find the value of unknown r in the following table.
| Faces | 8 |
| Vertices | 11 |
| Edges | r |
Can a polyhedron have V = F = 9 and E = 16? If yes, draw its figure.
A polyhedron has 60 edges and 40 vertices. Find the number of its faces.
