Advertisements
Advertisements
प्रश्न
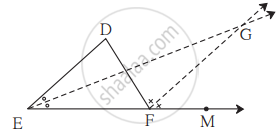
निचे दी गई आकृति के आधार पर रेख DE || रेख GF है । किरण EG तथा किरण FG क्रमशः ∠DEF तथा ∠DFM के समद्विभाजक है ।
- ∠DEG = `1/2∠"EDF"`
- EF = FG.
उत्तर
(i) ∠DEG = ∠FEG = x° ...(i) [रेखा EG, ∠DEF को समद्विभाजित करता है]
∠GFD = ∠GFM = y° ...(i) [रेखा FG ∠DFM को समद्विभाजित करता है]
लाइन DE || रेखा GF और DF उनकी तिर्यक रेखा है। ...[दिया गया]
∴ ∠EDF = ∠GFD ...[एकांतर कोण]
∴ ∠EDF = y° ...(iii) [(ii) से]
लाइन DE || रेखा GF और EM उनकी तिर्यक रेखा है। ...[दिया गया]
∴ ∠DEF = ∠GFM ...[संगत कोण]
∴ ∠DEG + ∠FEG = ∠GFM ...[कोण का योग ]
∴ x° + x° = y° ...[(i) और (ii) से]
∴ 2x° = y°
∴ x° = `1/2` y°
∴ ∠DEG = `1/2`∠EDF ...[(i) और (iii) से]
(ii) रेखा DE || रेखा GF और GE उनकी तिर्यक रेखा है। ...[दिया गया]
∴ ∠DEG = ∠FGE ...(iv) [एकांतर कोण]
∴ ∠FEG = x° ...(v) [(i) और (iv) से]
∴ ∆FEG में,
∠FEG = ∠FGE ... ...[(v) से]
∴ EF = FG ...[समद्विबाहु त्रिभुज प्रमेय ]
APPEARS IN
संबंधित प्रश्न
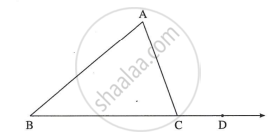
नीचे दी गई आकृति के आधार पर ∠ACD यह ΔABC का बहिष्कोण है।∠B = 40°, ∠A = 70°, तो m ∠ACD ज्ञात कीजिए।
ΔPQR मे ∠P = 70°, ∠Q = 65° तो ∠R का माप ज्ञात कीजिए।
त्रिभुज के कोणों के माप x°, (x - 20)°, (x - 40)° हों तो, प्रत्येक कोण का माप ज्ञात कीजिए।
निचे दी गई आकृति के आधार पर दिए गए कोणों के मापों के आधार पर x, y, z के मान ज्ञात कीजिए ।

निचे दी गई आकृति के पर रेखा AB || रेखा DE है । दिए गए मापों के आधार पर ∠DRE तथा ∠ARE के माप ज्ञात कीजिए ।

ΔABC में ∠A तथा ∠B के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि ∠C = 70° हो तो ∠AOB का माप ज्ञात कीजिए।
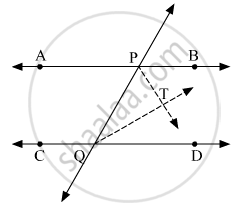
निचे दी के आकृति आधार पर रेखा AB || रेखा CD तथा रेखा PQ उनकी तिर्यक रेखा है। किरण PT तथा किरण QT क्रमशः ∠BPQ तथा ∠PQD के समद्विभाजक हैं, सिद्ध कीजिए कि ∠PTQ = 90°
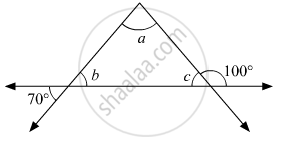
निचे दी आकृति के आधार पर ∠a, ∠b तथा ∠c के माप ज्ञात कीजिए।