Advertisements
Advertisements
प्रश्न
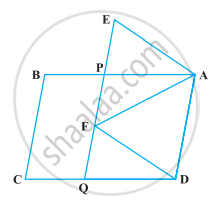
निम्नलिखित आकृति में, ABCD और AEFD दो समांतर चतुर्भुज हैं। सिद्ध कीजिए कि ar (PEA) = ar (QFD) है। [संकेत : PD को मिलाइए।]
योग
उत्तर
दिया गया है - ABCD और AEFD दो समांतर चतुर्भुज हैं।
सिद्ध करना है - ar (APEA) = ar (AQFD)
प्रमाण - चतुर्भुज PQDA में,
AP || DQ ...[चूँकि, समान्तर चतुर्भुज ABCD में, AB || CD]
और PQ || AD ...[चूँकि, समांतर चतुर्भुज AEFD में, FE || AD]
फिर, चतुर्भुज PQDA एक समांतर चतुर्भुज है।
साथ ही, समांतर चतुर्भुज PQDA और AEFD एक ही आधार AD पर और समान समांतर रेखाओं AD और EQ के बीच हैं।
ar (समांतर चतुर्भुज PQDA) = ar (समांतर चतुर्भुज AEFD)
दोनों ओर से ar (चतुर्भुज APFD) घटाने पर, हम पाते हैं।
ar (समांतर चतुर्भुज PQDA) – ar (चतुर्भुज APFD)
= ar (समांतर चतुर्भुज AEFD) - ar (चतुर्भुज APFD)
⇒ ar (AQFD) = ar (APEA)
अतः सिद्ध हुआ।
shaalaa.com
एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
