Advertisements
Advertisements
प्रश्न
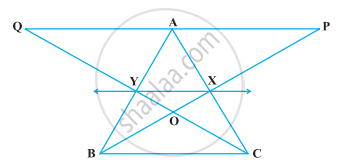
निम्नलिखित आकृति में, X और Y क्रमश : AC और AB के मध्य-बिंदु हैं, QP || BC और CYQ और BXP सरल रेखाएँ हैं। सिद्ध कीजिए कि ar (ABP) = ar (ACQ) हैं।
उत्तर
दिया गया है - X और Y क्रमश : AC और AB के मध्य-बिंदु हैं। साथ ही, QP || BC और CYQ, BXP सीधी रेखाएँ हैं।
सिद्ध करना है - ar (ΔABP) = ar (ΔACQ)
उपपत्ति - चूँकि X और Y क्रमश : AC और AB के मध्य-बिंदु हैं।
तो, XY || BC
हम जानते हैं कि, एक ही आधार और एक ही समांतर रेखाओं के बीच बने त्रिभुज क्षेत्रफल में बराबर होते हैं।
यहाँ, ΔBYC और ΔBXC एक ही आधार BC और समान समांतर रेखाओं BC और XY के बीच स्थित हैं।
इसलिए, ar (ΔBYC) = ar (ΔBXC)
दोनों ओर से ar (ΔBOC) घटाने पर, हम पाते हैं।
ar (ΔBYC) – ar (ΔBOC) = ar (ΔBXC) – ar (ΔBOC)
=» ar (ΔBOY) = ar (ΔCOX)
दोनों ओर से ar (ΔXOY) घटाने पर, हम पाते हैं।
ar (ΔSOY) + ar (ΔXOY) = ar (ΔCOX) + ar (ΔXOY)
⇒ ar (ΔBYX) = ar (ΔCXY) ...(i)
इसलिए, हम देखते हैं कि चतुर्भुज XYAP और YXAQ एक ही आधार XY पर और समान समांतर रेखाओं XY और PQ के बीच हैं।
ar (XYAP) = ar (YXAQ) ...(ii)
समीकरण (i) और (ii) को जोड़ने पर, हम पाते हैं।
ar (ΔBYX) + ar (XYAP) = ar (ΔCXY) + ar (YXAQ)
⇒ ar (ΔABP) = ar (ΔACQ)
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
P और Q एक समांतर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित कोई दो बिंदु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
एक किसान के पास समांतर चतुर्भुज PQRS के रूप में एक खेत था। उसने RS पर कोई बिंदु A लिया और उसे बिंदु P और Q से मिला दिया। क्षेत्र को कितने भागों में विभाजित किया गया है? इन भागों के आकार क्या हैं? किसान गेहूँ और दालों को खेत के बराबर भागों में अलग-अलग बोना चाहता है। उसे कैसे करना चाहिए?
दी गई आकृति में, ΔABC की माध्यिका AD पर स्थित E कोई बिंदु है। दिखाएँ कि ar (ABE) = ar (ACE) है।
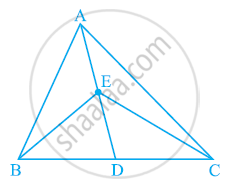
एक त्रिभुज ΔABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ar (BED) = `1/4`ar (ABC) है।
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है सिद्ध कीजिए कि ABCD एक समलंब है |
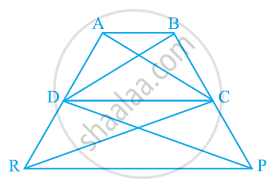
दी गई आकृति में, ar(DRC) = ar(DPC) है और ar(BDP) = ar(ARC) है | दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलंब है |
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर काटती है, तो दर्शाइए कि ar(BPC) = ax(DPQ)
[संकेत AC को मिलाइए।]
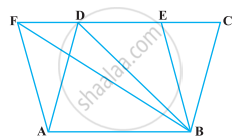
समांतर चतुर्भुज ABCD का क्षेत्रफल 90 cm2 है। ज्ञात कीजिए : ar (ΔBEF)
एक त्रिभुज ABC की माध्यिकाएँ BE और CF परस्पर बिंदु G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि ∆GBC का क्षेत्रफल चतुर्भुज AFGE के क्षेत्रफल के बराबर हैं।
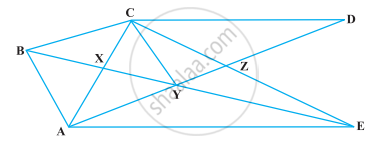
निम्नलिखित आकृति में, CD || AE और CY || BA है। सिद्ध कीजिए कि ar (CBX) = ar (AXY) है।