Advertisements
Advertisements
प्रश्न
यदि एक त्रिभुज ABC की माध्यिकाएँ G पर मिलती हैं, तो सिद्ध कीजिए कि ar (AGB) = ar (AGC) = ar (BGC) = `1/3` ar (ABC) हैं।
उत्तर
दिया गया है - ΔABC में, AD, BE और CF माध्यिकाएँ हैं और G पर प्रतिच्छेद करती हैं।
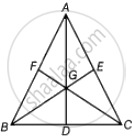
साबित करने के लिए - ar (ΔAGB) = ar (ΔAGC) = ar (ΔBGC) = `1/3` ar (ΔABC)
उपपत्ति - हम जानते हैं कि, त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
ΔABC में, AD एक माध्यिका है।
∴ ar (ΔABD) = ar (ΔACD) ...(i)
ΔBGC में, GD एक माध्यिका है।
∴ ar (ΔGBD) = ar (ΔGCD) ...(ii)
समीकरण (ii) को समीकरण (i) से घटाने पर, हम पाते हैं।
ar (ΔABD) – ar (ΔGBD) = ar (ΔACD) – ar (ΔGCD)
⇒ ar (ΔAGB) = ar (ΔAGC) ...(iii)
इसी प्रकार, ar (ΔAGB) = ar (ΔBGC) ...(iv)
समीकरण (iii) और (iv) से,
ar (ΔAGB) = ar (ΔBGC) = ar (ΔAGC) ...(v)
अब, ar (ΔABC) = ar (ΔAGB) + ar (ΔBGC) + ar (ΔAGC)
⇒ ar (ΔABC) = ar (ΔAGB) + ar (ΔAGB) + ar (ΔAGB) ...[समीकरण (v) से]
⇒ ar (ΔABC) = 3 ar (ΔAGB)
⇒ ar (ΔAGB) = `1/3` ar (ΔABC) ...(vi)
समीकरण (v) और (vi) से,
ar (ΔBGC) = `1/3` ar (ΔABC)
और ar (ΔAGC) = `1/3` ar (ΔABC)
अतः सिद्ध हुआ।