Advertisements
Advertisements
प्रश्न
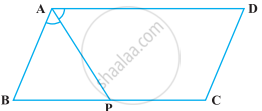
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD की भुजा BC पर एक बिंदु P इस प्रकार स्थित है। कि ∠BAP = ∠DAP है। सिद्ध कीजिए कि AD = 2CD है।
उत्तर
प्रश्न में दिया गया है, समान्तर चतुर्भुज ABCD में, P, BC का मध्य-बिन्दु इस प्रकार है कि ∠BAP = ∠DAP है।
सिद्ध करना है कि AD = 2CD
उपपत्ति - ABCD एक समांतर चतुर्भुज है।
तो, AD || BC और AB तिर्यक रेखा है, तो
∠A + ∠B = 180° ...[सहआंतरिक कोणों का योग 180° होता है।]
∠B = 180° – ∠A ...(i)
अब, त्रिभुज ABP में,
∠PAB + ∠B + ∠BPA = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
`1/2 ∠A + 180^circ - ∠A + ∠BPA = 180^circ` ...[समीकरण (i) से]
`∠BPA - (∠A)/2 = 0`
`∠BPA = (∠A)/2` ...(ii)
∠BPA = ∠BAP
AB = BP ...[समान कोणों की सम्मुख भुजाएँ बराबर होती हैं।]
उपरोक्त समीकरण में दोनों पक्षों को 2 से गुणा करने पर, हम प्राप्त करते हैं।
2AB = 2BP
2AB = BC ...[P, BC का मध्य-बिंदु है।]
2CD = AD ...[ABCD एक समांतर चतुर्भुज है, तो AB = CD और BC = AD]
APPEARS IN
संबंधित प्रश्न
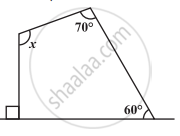
निम्नलिखित आकृति में x (कोण की माप) ज्ञात कीजिए :
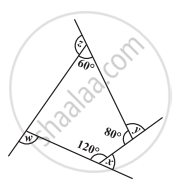
x + y + z + w ज्ञात कीजिए।
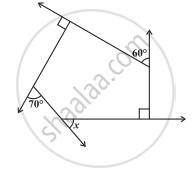
निम्नलिखित आकृति में x का मान ज्ञात कीजिए:
D और E क्रमश : ∆ABC की भुजा AB और AC के मध्य-बिंदु हैं। DE को F तक बढ़ाया जाता है। यह सिद्ध करने के लिए कि CF रेखाखंड DA के बराबर और समांतर है। हमें एक अतिरिक्त सूचना की आवश्यकता है, जो है ______।
क्या किसी चतुर्भुज के सभी कोण अधिककोण हो सकते हैं? अपने उत्तर के लिए कारण दीजिए।
कोई वर्ग एक समद्विबाहु समकोण त्रिभुज के अंतर्गत इस प्रकार है कि वर्ग और त्रिभुज में एक कोण उभयनिष्ठ है। दर्शाइए कि वर्ग का शीर्ष जो उभयनिष्ठ कोण के शीर्ष के सम्मुख है कर्ण को समद्विभाजित करता है।
किसी चतुर्भुज के कोण 1 : 2 : 3 : 4 के अनुपात में हैं। इनमें सबसे छोटा कोण है –
चतुर्भुज के सभी ______ का योग 360∘ है।
वह बहुभुज, जिसमें एक ही क्रम में लिये गये सभी बहिष्कोणों का योग उसके अंतःकोणों के योग के बराबर हो, एक ______ होता है।
चतुर्भुज PQRS में, ∠P = 50∘, ∠Q = 50∘ और ∠R = 60∘ है। ∠S ज्ञात कीजिए। क्या यह चतुर्भुज उत्तल है या अवतल?
