Advertisements
Advertisements
प्रश्न
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
`1/15,1/12,1/10`, ...., 11 पदों तक
उत्तर
`1/15,1/12,1/10`, ...., 11 पदों तक
इस A.P. के लिए,
a = `1/15`
n = 11
d = a2 - a1
= `1/12-1/15`
= `(5-4)/60`
= `1/60`
हम जानते हैं कि
Sn = `n/2[2a + (n -1)d]`
S11 = `11/2[2(1/15)+(11-1)1/60]`
S11 = `11/2[2/5+10/60]`
S11 = `11.2[2/15+1/6]`
S11 = `11/2[(4+5)/30]`
S11 = `(11/2)(9/30)`
S11 = `33/20`
इस प्रकार, पहले 11 पदों का अपेक्षित योग `33/20` है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित समांतर श्रेढ़ी का योग ज्ञात कीजिए:
0.6, 1.7, 2.8, ....,100 पदों तक
एक A.P. में, a12 = 37 और d = 3 दिया है। a और S12 ज्ञात कीजिए।
एक A.P. में, d = 5 और S9 = 75 दिया है। a और a9 ज्ञात कीजिए।
एक A.P. में, a = 3, n = 8 और S = 192 दिया है। d ज्ञात कीजिए।
0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
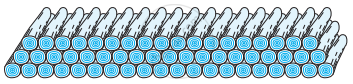
200 लट्ठों (logs) को ढेरी के रूप में इस प्रकार रखा जाता है : सबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे, उससे अगली पंक्ति में 18 लट्ठे, इत्यादि (देखिए आकृति)। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
ज्ञात कीजिए :
1 से 500 तक के उन पूर्णांकों का योग जो 2 के भी गुणज हैं और 5 के भी गुणज हैं।
ज्ञात कीजिए :
1 से 500 तक के उन पूर्णांकों का योग जो 2 या 5 के गुणज हैं।
[संकेत (iii) : ये संख्याएँ होंगी : 2 के गुणज + 5 के गुणज – 2 और 5 दोनों के गुणज]
100 और 200 के बीच के उन पूर्णांकों का योग ज्ञात कीजिए, जो 9 से विभाज्य नहीं हैं।
[संकेत (ii) : ये संख्याएँ होंगी : कुल संख्याएँ– 9 से विभाज्य संख्याएँ]
दर्शाइए कि उस AP का योग, जिसका प्रथम पद a, द्वितीय पद b और अंतिम पद c हो, `((a + c)(b + c - 2a))/(2(b - a))` के बराबर है।
