Advertisements
Advertisements
प्रश्न
Obtain Bohr’s quantisation condition for angular momentum of electron orbiting in nth orbit in hydrogen atom on the basis of the wave picture of an electron using de Broglie hypothesis.
उत्तर १
`n lambda = 2 pi r`
But ` lambda = n/(mv) `( By De Broglie)
`(n lambda) /(mv) = 2 pi r`
` therefore (lambda n) /(2 pi ) = mvr ` (mvr = L)
` therefore L = (lambda n)/(2 pi)`
उत्तर २
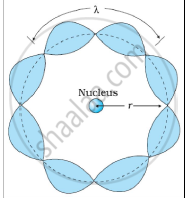
Bohr's second postulate states that the angular momentum of an electron has only those values that are integral multiples of `"h"/(2pi)` He thought that the motion of electrons within an atom is associated with the standing wave along the orbit as shown.
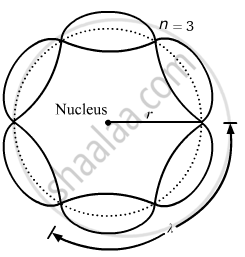
About standing waves in stretched strings, we know that only those waves survive for which the distances traveled in the round trip between the ends are integral multiples of the wavelength. Similarly, for an electron moving in the nth orbit of radius rn, the distance traveled in one trip is 2πrn, which should be an integral multiple of the wavelength.
2πrn = nλ (where n= 1, 2, 3, 4 etc)
By de-Broglie hypothesis, we have:
`lambda = "h"/"p" = "h"/("mv"_"n")`
Substituting the value of λ in the above expression, we get:
`2pi"r"_"n" = "n" "h"/"mv"_"n"`
⇒ `"mv"_"n""r"_"n" = "n" "h"/(2pi)`
Angular momentum `= "L" = "n" "h"/(2pi)`
संबंधित प्रश्न
What is the maximum number of emission lines when the excited electron of an H atom in n = 6 drops to the ground state?
The ratio of kinetic energy of an electron in Bohr’s orbit to its total energy in the same orbit is
(A) – 1
(B) 2
(C) 1/2
(D) – 0.5
(a) Using the Bohr’s model calculate the speed of the electron in a hydrogen atom in the n = 1, 2, and 3 levels.
(b) Calculate the orbital period in each of these levels.
Using Bohr’s postulates, obtain the expression for total energy of the electron in the nth orbit of hydrogen atom.
If the radius of first electron orbit in hydrogen atom be r then the radius of the fourth orbit ill be ______.
When an electric discharge is passed through hydrogen gas, the hydrogen molecules dissociate to produce excited hydrogen atoms. These excited atoms emit electromagnetic radiation of discrete frequencies which can be given by the general formula
`bar(v) = 109677 1/n_1^2 - 1/n_f^2`
What points of Bohr’s model of an atom can be used to arrive at this formula? Based on these points derive the above formula giving description of each step and each term.
On the basis of Bohr's model, the approximate radius of Li++ ion in its ground state ifthe Bohr radius is a0 = 53 pm :
In Bohr's atomic model of hydrogen, let K. P and E are the kinetic energy, potential energy and total energy of the electron respectively. Choose the correct option when the electron undergoes transitions to a higher level:
According to Bohr atom model, in which of the following transitions will the frequency be maximum?
On the basis of Bohr's theory, derive an expression for the radius of the nth orbit of an electron of hydrogen atom.
