Advertisements
Advertisements
प्रश्न
Obtain Bohr’s quantisation condition for angular momentum of electron orbiting in nth orbit in hydrogen atom on the basis of the wave picture of an electron using de Broglie hypothesis.
उत्तर १
`n lambda = 2 pi r`
But ` lambda = n/(mv) `( By De Broglie)
`(n lambda) /(mv) = 2 pi r`
` therefore (lambda n) /(2 pi ) = mvr ` (mvr = L)
` therefore L = (lambda n)/(2 pi)`
उत्तर २
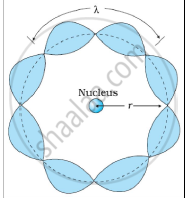
Bohr's second postulate states that the angular momentum of an electron has only those values that are integral multiples of `"h"/(2pi)` He thought that the motion of electrons within an atom is associated with the standing wave along the orbit as shown.
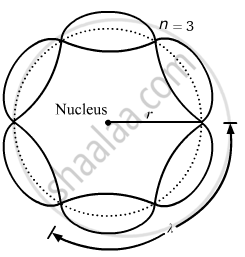
About standing waves in stretched strings, we know that only those waves survive for which the distances traveled in the round trip between the ends are integral multiples of the wavelength. Similarly, for an electron moving in the nth orbit of radius rn, the distance traveled in one trip is 2πrn, which should be an integral multiple of the wavelength.
2πrn = nλ (where n= 1, 2, 3, 4 etc)
By de-Broglie hypothesis, we have:
`lambda = "h"/"p" = "h"/("mv"_"n")`
Substituting the value of λ in the above expression, we get:
`2pi"r"_"n" = "n" "h"/"mv"_"n"`
⇒ `"mv"_"n""r"_"n" = "n" "h"/(2pi)`
Angular momentum `= "L" = "n" "h"/(2pi)`
संबंधित प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
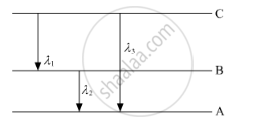
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state? The ground state electron energy is –2.18 × 10–11 ergs.
The numerical value of ionization energy in eV equals the ionization potential in volts. Does the equality hold if these quantities are measured in some other units?
Calculate the magnetic dipole moment corresponding to the motion of the electron in the ground state of a hydrogen atom.
According to Bohr, 'Angular momentum of an orbiting electron is quantized'. What is meant by this statement?
Answer the following question.
Calculate the de-Broglie wavelength associated with the electron revolving in the first excited state of the hydrogen atom. The ground state energy of the hydrogen atom is – 13.6 eV.
The wavelength of the first time line of Ballmer series is 6563 A°. The Rydberg constant for hydrogen is about:-
A 100 eV electron collides with a stationary helium ion (He+) in its ground state and exits to a higher level. After the collision, He+ ions emit two photons in succession with wavelengths 1085 Å and 304 Å. The energy of the electron after the collision will be ______ eV.
Given h = 6.63 × 10-34 Js.
A 20% efficient bulb emits light of wavelength 4000 Å. If the power of the bulb is 1 W, the number of photons emitted per second is ______.
[Take, h = 6.6 × 10-34 J-s]
The wavelength of the second line of the Balmer series in the hydrogen spectrum is 4861 Å. Calculate the wavelength of the first line of the same series.
