Advertisements
Advertisements
प्रश्न
What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state? The ground state electron energy is –2.18 × 10–11 ergs.
उत्तर
Energy (E) of the nth Bohr orbit of an atom is given by,
`"E"_"n" = (-(2.18xx10^(-18))"Z"^2)/"n"^2`
Where,
Z = atomic number of the atom
Ground state energy = – 2.18 × 10–11 ergs
= - 2.18 × 10–11 × 10–7 J
= - 2.18 × 10–18 J
Energy required to shift the electron from n = 1 to n = 5 is given as:
ΔE = E5 – E1
`= (-(2.18xx10^(-18))(1)^2)/(5)^2 - (-2.18 xx 10^(-18))`
`= (2.18xx10^(-18))[1 - 1/25]`
`= (2.18xx10^(-18))(24/25)`
`= 2.0928 xx 10^(-18)"J"`
Wavelength of emitted light = `"hc"/"E"`
`= ((6.626xx10^(-34))(3xx10^(8)))/(2.0928xx10^(-18))`
`= 9.498 xx 10^(-8) "m"`
APPEARS IN
संबंधित प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
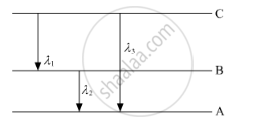
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
The energy associated with the first orbit in the hydrogen atom is - 2.18 × 10-18 J atom-1. What is the energy associated with the fifth orbit?
Explain, giving reasons, which of the following sets of quantum numbers are not possible.
(a) n = 0, l = 0, ml = 0, ms = + ½
(b) n = 1, l = 0, ml = 0, ms = – ½
(c) n = 1, l = 1, ml = 0, ms = + ½
(d) n = 2, l = 1, ml = 0, ms = – ½
(e) n = 3, l = 3, ml = –3, ms = + ½
(f) n = 3, l = 1, ml = 0, ms = + ½
How many electrons in an atom may have the following quantum numbers?
n = 3, l = 0
The ratio of kinetic energy of an electron in Bohr’s orbit to its total energy in the same orbit is
(A) – 1
(B) 2
(C) 1/2
(D) – 0.5
The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10−11 m. What are the radii of the n = 2 and n = 3 orbits?
if `E_p` and `E_k` represent potential energy and kinetic energy respectively, of an orbital electron, then, according to B9hr's theory:
a)`E_k = -E_p"/"2`
b) `E_k = -E_p`
c) `E_k = -2E_p`
d) `E_k = 2E_p`
Using Bohr’s postulates, obtain the expression for total energy of the electron in the nth orbit of hydrogen atom.
The Bohr radius is given by `a_0 = (∈_0h^2)/{pime^2}`. Verify that the RHS has dimensions of length.
Evaluate Rydberg constant by putting the values of the fundamental constants in its expression.
Radiation from hydrogen discharge tube falls on a cesium plate. Find the maximum possible kinetic energy of the photoelectrons. Work function of cesium is 1.9 eV.
The energy associated with the first orbit of He+ is ____________ J.
Derive an expression for the frequency of radiation emitted when a hydrogen atom de-excites from level n to level (n – 1). Also show that for large values of n, this frequency equals to classical frequency of revolution of an electron.
The wavelength of the first time line of Ballmer series is 6563 A°. The Rydberg constant for hydrogen is about:-
The ground state energy of hydrogen atoms is -13.6 eV. The photon emitted during the transition of electron from n = 3 to n = 1 unknown work function. The photoelectrons are emitted from the material with a maximum kinetic energy of 9 eV. Calculate the threshold wavelength of the material used.
A hydrogen atom in its first excited state absorbs a photon of energy x × 10-2 eV and exited to a higher energy state where the potential energy of electron is -1.08 eV. The value of x is ______.
What is the energy associated with first orbit of Li2+ (RH = 2.18 × 10-18)?
An electron in a hydrogen atom has an energy of -3.4 eV. The difference between its kinetic and potential energy is ______.
The radius of the nth orbit in the Bohr model of hydrogen is proportional to ______.
