Advertisements
Advertisements
Question
Obtain Bohr’s quantisation condition for angular momentum of electron orbiting in nth orbit in hydrogen atom on the basis of the wave picture of an electron using de Broglie hypothesis.
Solution 1
`n lambda = 2 pi r`
But ` lambda = n/(mv) `( By De Broglie)
`(n lambda) /(mv) = 2 pi r`
` therefore (lambda n) /(2 pi ) = mvr ` (mvr = L)
` therefore L = (lambda n)/(2 pi)`
Solution 2
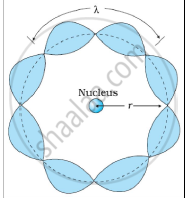
Bohr's second postulate states that the angular momentum of an electron has only those values that are integral multiples of `"h"/(2pi)` He thought that the motion of electrons within an atom is associated with the standing wave along the orbit as shown.
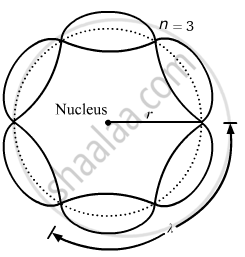
About standing waves in stretched strings, we know that only those waves survive for which the distances traveled in the round trip between the ends are integral multiples of the wavelength. Similarly, for an electron moving in the nth orbit of radius rn, the distance traveled in one trip is 2πrn, which should be an integral multiple of the wavelength.
2πrn = nλ (where n= 1, 2, 3, 4 etc)
By de-Broglie hypothesis, we have:
`lambda = "h"/"p" = "h"/("mv"_"n")`
Substituting the value of λ in the above expression, we get:
`2pi"r"_"n" = "n" "h"/"mv"_"n"`
⇒ `"mv"_"n""r"_"n" = "n" "h"/(2pi)`
Angular momentum `= "L" = "n" "h"/(2pi)`
RELATED QUESTIONS
if `E_p` and `E_k` represent potential energy and kinetic energy respectively, of an orbital electron, then, according to B9hr's theory:
a)`E_k = -E_p"/"2`
b) `E_k = -E_p`
c) `E_k = -2E_p`
d) `E_k = 2E_p`
Balmer series was observed and analysed before the other series. Can you suggest a reason for such an order?
State any two Bohr’s postulates and write the energy value of the ground state of the hydrogen atom.
Write postulates of Bohr’s Theory of hydrogen atom.
In Bohr model of hydrogen atom, which of the following is quantised?
According to Bhor' s theory the moment of momentum of an electron revolving in second orbit of hydrogen atom will be.
A hydrogen atom in its first excited state absorbs a photon of energy x × 10-2 eV and exited to a higher energy state where the potential energy of electron is -1.08 eV. The value of x is ______.
Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-Broglie wavelengths of the particle. For a charged particle moving in a plane perpendicular to a magnetic field, the radius of the nth orbital will therefore be proportional to:
A 20% efficient bulb emits light of wavelength 4000 Å. If the power of the bulb is 1 W, the number of photons emitted per second is ______.
[Take, h = 6.6 × 10-34 J-s]
On the basis of Bohr's theory, derive an expression for the radius of the nth orbit of an electron of hydrogen atom.
