Advertisements
Advertisements
प्रश्न
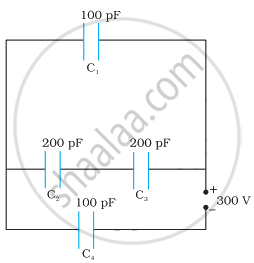
Obtain the equivalent capacitance of the network in Figure. For a 300 V supply, determine the charge and voltage across each capacitor.
उत्तर
Capacitance of capacitor C1 is 100 pF.
Capacitance of capacitor C2 is 200 pF.
Capacitance of capacitor C3 is 200 pF.
Capacitance of capacitor C4 is 100 pF.
Supply potential, V = 300 V
Capacitors C2 and C3 are connected in series.
Let their equivalent capacitance be C'
∴ `1/"C'" = 1/200 + 1/200 = 2/200`
∴ C' = 100 pF
Capacitors C1 and C' are in parallel. Let their equivalent capacitance be C''.
∴ `"C''" = "C'" + "C"_1`
= 100 + 100
= 200 pF
C'' and C4 are connected in series. Let their equivalent capacitance be C.
∴ `1/C = 1/("C''") + 1/("C"_4)`
= `1/200 + 1/100`
= `(2 + 1)/200`
C = `200/3` pF
Hence, the equivalent capacitance of the circuit is `200/3` pF.
Potential difference across C" = V"
Potential difference across C4 = V4
∴ `"V''" + "V"_4 = "V" = 300 "V"`
Charge on C4 is given by
Q4 = CV
= `200/3 xx 10^-12 xx 300`
= `2 xx 10^-8 "C"`
∴ `"V"_4 = "Q"_4/"C"_4`
= `(2 xx 10^-8)/(100 xx 10^-12)` = 200 V
∴ Voltage across C1 is given by
`"V"_1 = "V" - "V"_4`
= `300 - 200 = 100 "V"`
Hence, potential difference, V1, across C1 is 100 V.
Charge on C1 is given by,
`"Q"_1 = "C"_1"V"_1`
= `100 xx 10^-12 xx 100`
= `10^-8 "C"`
C2 and C3 have the same capacitances have a potential difference of 100 V together. Since C2 and C3 are in series, the potential difference across C2 and C3 is given by,
V2 = V3 = 50 V
Therefore, charge on C2 is given by,
`"Q"_2 = "C"_2"V"_2`
= `200 xx 10^-12 xx 50`
= `10^-8 "C"`
And charge on C3 is given by,
`"Q"_3 = "C"_3"V"_3`
= `200 xx 10^-12 xx 50`
= `10^-8 "C"`
Hence, the equivalent capacitance of the given circuit is `200/3` pF with
Q1 = 10−8 C, V1 = 100 V
Q2 = 10−8 C, V2 = 50 V
Q3 = 10−8 C, V3 = 50 V
Q4 = 2 × 10−8 C, V4 = 200 V
APPEARS IN
संबंधित प्रश्न
A capacitor of capacitance C is charged fully by connecting it to a battery of emf E. It is then disconnected from the battery. If the separation between the plates of the capacitor is now doubled, how will the following change?
(i) charge stored by the capacitor.
(ii) Field strength between the plates.
(iii) Energy stored by the capacitor.
Justify your answer in each case.
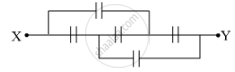
Find the equivalent capacitance of the network shown in the figure, when each capacitor is of 1 μF. When the ends X and Y are connected to a 6 V battery, find out (i) the charge and (ii) the energy stored in the network.
Define capacitor reactance. Write its S.I units.
The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
Find the charges on the three capacitors connected to a battery as shown in figure.
Take `C_1 = 2.0 uF , C_2 = 4.0 uF , C_3 = 6.0 uF and V` = 12 volts.

Two conducting spheres of radii R1 and R2 are kept widely separated from each other. What are their individual capacitances? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series−parallel connections.
A cylindrical capacitor is constructed using two coaxial cylinders of the same length 10 cm and of radii 2 mm and 4 mm. (a) Calculate the capacitance. (b) Another capacitor of the same length is constructed with cylinders of radii 4 mm and 8 mm. Calculate the capacitance.
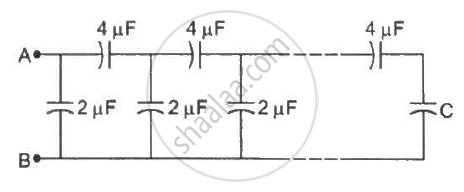
A finite ladder is constructed by connecting several sections of 2 µF, 4 µF capacitor combinations as shown in the figure. It is terminated by a capacitor of capacitance C. What value should be chosen for C, such that the equivalent capacitance of the ladder between the points A and B becomes independent of the number of sections in between?
The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
Three capacitors C1 = 3μF, C2 = 6μF, and C3 = 10μF are connected to a 50 V battery as shown in Figure below:

Calculate:
(i) The equivalent capacitance of the circuit between points A and B.
(ii) The charge on C1.
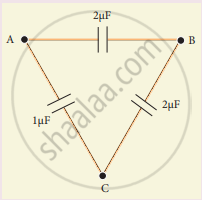
Three capacitors are connected in a triangle as shown in the figure. The equivalent capacitance between points A and C is ______.
Obtain the expression for capacitance for a parallel plate capacitor.
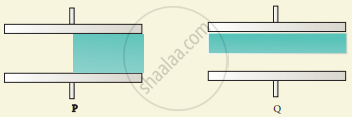
Capacitors P and Q have identical cross-sectional areas A and separation d. The space between the capacitors is filled with a dielectric of dielectric constant Er as shown in the figure. Calculate the capacitance of capacitors P and Q.
The work done in placing a charge of 8 × 10–18 coulomb on a condenser of capacity 100 micro-farad is ______.
A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V–1. A similar capacitor with no dielectric is charged to U0 = 78V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
A capacitor has charge 50 µC. When the gap between the plate is filled with glass wool, then 120 µC charge flows through the battery to capacitor. The dielectric constant of glass wool is ______.
A capacitor with capacitance 5µF is charged to 5 µC. If the plates are pulled apart to reduce the capacitance to 2 µF, how much work is done?
Calculate equivalent capacitance of the circuit shown in the Figure given below: