Advertisements
Advertisements
प्रश्न
Obtain an expression for an intensity of electric field at a point at the end of position, i.e., the axial position of an electric dipole.
x
उत्तर
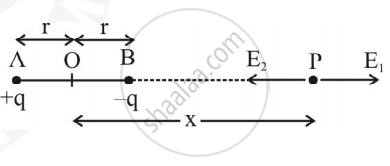
Consider an electric dipole consisting of charges –q and +q separated by a small distance 2r in free space.
Let P be a point on the axial line of the dipole at a distance x from the centre O of the dipole.
(i.e OP = x)
Electric field intensity at point P due to +q charge
`E_1 = 1/(4piepsilon_0).q/(AP^2)` (direction A to P)
`e_1 = 1/(4piepsilon_0).q/(x+r)^2` (direction A to P) ...(1)
Electric field intensity at point P due to –q charge
`E_2 = 1/(4piepsilon_0).q/(BP^2)` (direction P to B)
`E_2 = 1/(4piepsilon_0).q/(x-r)^2` (direction P to B) ...(2)
Since E2 > E1 and they act in opposite directions, resultant field intensity is given by :
E = E2 - E1 (direction P to B)
`= 1/(4piepsilon_0).q/(x-r)^2 - 1/(4piepsilon_0) .q/(x+r)^2`
`= 1/(4piepsilon_0).q[1/(x-r^2) - 1/(x+r)^2]`
`= 1/(4piepsilon_0).q[((x+r)^2 -(x-r)^2)/((x-r)^2 (x+r)^2)]`
`=1/4piepsilon_0.q[((x+r+x-r)(x+r-x+r))/(xx^2-r^2)^2]`
`= 1/4piepsilon_0.q [(2x.2r)/(x^2-r^2)^2]`
`E= 1/(4piepsilon_0). (2xp)/(x^2-r^2)^2 `[∵ p = 2r.q]
If the dipole is short (i.e., r << x) then r2 may be neglected as compared to x2
`E = 1/(4piepsilon_0) . (2p)/x^3`
The direction of resultant electric field E is along the dipole axis i.e., from –q charge to +q charge.
APPEARS IN
संबंधित प्रश्न
In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Å:
(a) Estimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is taken at 1.06 Å separation?
The electrostatic potential energy of two-point charges, 1 µC each, placed 1 meter apart in the air is:
Two-point charges placed in a medium of dielectric constant 5 are at a distance r between them, experience an electrostatic force ‘F’. The electrostatic force between them in vacuum at the same distance r will be ____________.
If stretch in a spring of force constant k is tripled then the ratio of elastic potential energy in the two cases will be:
Potential energy of two equal negative point charges 2µc each held lm apart in air is:-
In a region of constant potential ______.
- the electric field is uniform
- the electric field is zero
- there can be no charge inside the region
- the electric field shall necessarily change if a charge is placed outside the region
