Advertisements
Advertisements
प्रश्न
- Obtain the expression for the electric field intensity due to a uniformly charged spherical shell of radius R at a point distant r from the centre of the shell outside it.
- Draw a graph showing the variation of electric field intensity E with r, for r > R and r < R.
उत्तर
Electric field due to a uniformly charged thin spherical shell:
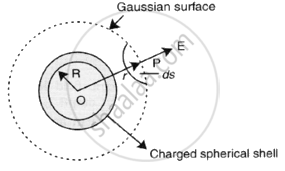
i. When point P lies outside the spherical shell: Suppose that we have calculate the field at point P at a distance r(r > R) from its centre. Draw the Gaussian surface through point P so as to enclose the charged spherical shell. The gaussian surface is a spherical surface of radius r and centre O.
Let `vecE` be the electric field at point P, then the electric flux through the area element of area `vec(ds)` is given by dφ = `vecE.vec(ds)`
Since `vec(ds)` is also along normal to the surface dφ = E dS
∴ Total electric flux through the Gaussian surface is given by
φ = `oint Eds = E point ds`
Now, `oint` ds = 4πr2 ...(i)
= E × 4πr2
Since the charge enclosed by the Gaussian surface is q, according to Gauss’s theorem,
φ = `q/∈_0` ...(ii)
From equations (i) and (ii) we obtain
E × 4πr2 = `q/∈_0`
E = `1/(4π∈_0) . q/r^2` ...(For r > R)
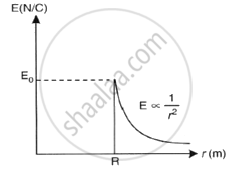
ii. A graph showing the variation of electric field as a function of r is shown below.
APPEARS IN
संबंधित प्रश्न
"For any charge configuration, equipotential surface through a point is normal to the electric field." Justify.
A point charge of 2.0 μC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Electric intensity outside a charged cylinder having the charge per unit length 'λ' at a distance from its axis is ________.
(a) E = `(2pi in_0 lambda)/(Kr^2)`
(b) E = `(in_0 lambda)/(2piKr^2)`
(c) E = `lambda/(2piin_0Kr)`
(d) E = `(4piin_0lambda)/(Kr^2)`
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown the figure. Use Gauss' law to obtain the expression for the electric flux through the square.
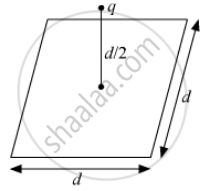
If the point charge is now moved to a distance 'd' from the centre of the square and the side of the square is doubled, explain how the electric flux will be affected.
If the ratio of radii of two wires of same material is 3 : 1 and ratio of their lengths is 5 : 1, then the ratio of the normal forces that will produce the same extension in the length of two wires is:
The electric field inside a spherical shell of uniform surface charge density is ______.
What is the nature of the Gaussian surface involved in the Gauss law of electrostatics?
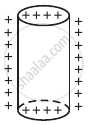
Sketch the electric field lines for a uniformly charged hollow cylinder shown in figure.