Advertisements
Advertisements
Question
- Obtain the expression for the electric field intensity due to a uniformly charged spherical shell of radius R at a point distant r from the centre of the shell outside it.
- Draw a graph showing the variation of electric field intensity E with r, for r > R and r < R.
Solution
Electric field due to a uniformly charged thin spherical shell:
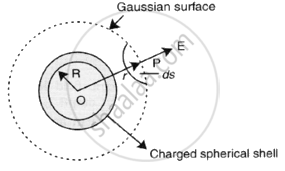
i. When point P lies outside the spherical shell: Suppose that we have calculate the field at point P at a distance r(r > R) from its centre. Draw the Gaussian surface through point P so as to enclose the charged spherical shell. The gaussian surface is a spherical surface of radius r and centre O.
Let `vecE` be the electric field at point P, then the electric flux through the area element of area `vec(ds)` is given by dφ = `vecE.vec(ds)`
Since `vec(ds)` is also along normal to the surface dφ = E dS
∴ Total electric flux through the Gaussian surface is given by
φ = `oint Eds = E point ds`
Now, `oint` ds = 4πr2 ...(i)
= E × 4πr2
Since the charge enclosed by the Gaussian surface is q, according to Gauss’s theorem,
φ = `q/∈_0` ...(ii)
From equations (i) and (ii) we obtain
E × 4πr2 = `q/∈_0`
E = `1/(4π∈_0) . q/r^2` ...(For r > R)
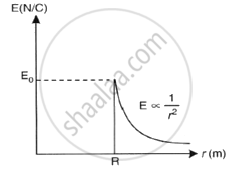
ii. A graph showing the variation of electric field as a function of r is shown below.
APPEARS IN
RELATED QUESTIONS
Explain why, for a charge configuration, the equipotential surface through a point is normal to the electric field at that point
"For any charge configuration, equipotential surface through a point is normal to the electric field." Justify.
A point charge of 2.0 μC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
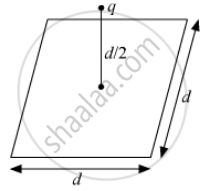
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown the figure. Use Gauss' law to obtain the expression for the electric flux through the square.
Draw a graph to show the variation of E with perpendicular distance r from the line of charge.
The electric field intensity outside the charged conducting sphere of radius ‘R’, placed in a medium of permittivity ∈ at a distance ‘r’ from the centre of the sphere in terms of surface charge density σ is
A spherical ball contracts in volume by 0.02% when subjected to a pressure of 100 atmosphere. Assuming one atmosphere = 105 Nm−2, the bulk modulus of the material of the ball is:
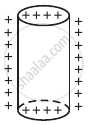
Sketch the electric field lines for a uniformly charged hollow cylinder shown in figure.
A solid metal sphere of radius R having charge q is enclosed inside the concentric spherical shell of inner radius a and outer radius b as shown in the figure. The approximate variation of the electric field `vecE` as a function of distance r from centre O is given by ______.

