Advertisements
Advertisements
Question
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Solution
Take a long thin wire XY (as shown in the figure) of uniform linear charge density `lambda`.

Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure.
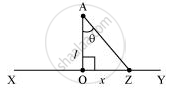
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
∴ `"q" = lambda "dx"`
Electric field due to the piece,
`"dE" = 1/(4piin_0)(lambda "dx")/(("AZ")^2)`
However, `"AZ" = sqrt(("l"^2 + "x"^2))`
`"dE"= ( lambda "dx")/(4piin_0("l"^2 + "x"^2))`
The electric field is resolved into two rectangular components. `"dE"cos theta` is the perpendicular component and `"dE"sintheta` is the parallel component.
When the whole wire is considered, the component `"dE"sintheta` is cancelled.
Only the perpendicular component `"dE"cos theta` affects point A.
Hence, effective electric field at point A due to the element dx is dE1.
∴ `"dE"_1 = (lambda"dx" costheta)/(4piin_0("x"^2 + "l"^2))` .............(1)
In `triangle"AZO",`
`tantheta = "x"/"l"`
`"x" = "l" tantheta` ............(2)
On differentiating equation (2), we obtain `("dx")/("d" theta)= "l"sec^2theta`
`"dx" = "l"sec^2theta "d"theta` ........(3)
From equation (2),
`"x"^2 + "l"^2 = "l"^2 + "l"^2 tan theta`
∴ `"l"^2(1 + tan^2 theta) = "l"^2sec^2theta`
∴ `"x"^2 + "l"^2 = "l"^2sin^2theta` ........(4)
Putting equations (3) and (4) in equation (1), we obtain
∴ `"dE"_1= ( lambda "l" sec^2 "d" theta)/(4piin_0"l"^2sec^2 theta) xx costheta`
∴ `"dE"_1 = (lambda cos theta "d" theta)/(4 pi in_0 "l")` ..............(5)
The wire is so long that `theta` tends from `-pi/2` to `+pi/2`.
By integrating equation (5), we obtain the value of field E1 as,
`int_(-pi/2)^(pi/2) "dE"_1 = int_(-pi/2)^(pi/2)lambda/(4piin_0"l") cos theta "d" theta`
`"E"_1 = lambda/(4piin_0"l")[sin theta]_(-pi/2)^(pi/2)`
= `lambda/(4 pi in_0"l") xx 2`
`"E"_1 = lambda/(2piin_0"l")`
Therefore, the electric field due to long wire is `lambda/(2piin_0"l")`.
APPEARS IN
RELATED QUESTIONS
Explain why, for a charge configuration, the equipotential surface through a point is normal to the electric field at that point
"For any charge configuration, equipotential surface through a point is normal to the electric field." Justify.
A point charge causes an electric flux of −1.0 × 103 Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge.
- If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?
- What is the value of the point charge?
Electric intensity outside a charged cylinder having the charge per unit length 'λ' at a distance from its axis is ________.
(a) E = `(2pi in_0 lambda)/(Kr^2)`
(b) E = `(in_0 lambda)/(2piKr^2)`
(c) E = `lambda/(2piin_0Kr)`
(d) E = `(4piin_0lambda)/(Kr^2)`
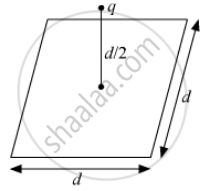
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown the figure. Use Gauss' law to obtain the expression for the electric flux through the square.
Use Gauss' law to derive the expression for the electric field `(vecE)` due to a straight uniformly charged infinite line of charge density λ C/m.
Draw a graph to show the variation of E with perpendicular distance r from the line of charge.
Find the work done in bringing a charge q from perpendicular distance r1 to r2 (r2 > r1)
The electric field intensity outside the charged conducting sphere of radius ‘R’, placed in a medium of permittivity ∈ at a distance ‘r’ from the centre of the sphere in terms of surface charge density σ is
A spherical ball contracts in volume by 0.02% when subjected to a pressure of 100 atmosphere. Assuming one atmosphere = 105 Nm−2, the bulk modulus of the material of the ball is:
Through two parallel wires A and B, 10A and 2A of currents are passed respectively in opposite directions. If the wire A is infinitely long and the length of the wire B is 2m, then force on the conductor B, which is situated at 10 cm distance from A, will be:
If the ratio of radii of two wires of same material is 3 : 1 and ratio of their lengths is 5 : 1, then the ratio of the normal forces that will produce the same extension in the length of two wires is:
What is the nature of the Gaussian surface involved in the Gauss law of electrostatics?
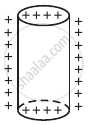
Sketch the electric field lines for a uniformly charged hollow cylinder shown in figure.