Advertisements
Advertisements
प्रश्न
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
उत्तर
Take a long thin wire XY (as shown in the figure) of uniform linear charge density `lambda`.

Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure.
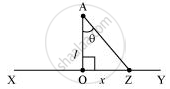
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
∴ `"q" = lambda "dx"`
Electric field due to the piece,
`"dE" = 1/(4piin_0)(lambda "dx")/(("AZ")^2)`
However, `"AZ" = sqrt(("l"^2 + "x"^2))`
`"dE"= ( lambda "dx")/(4piin_0("l"^2 + "x"^2))`
The electric field is resolved into two rectangular components. `"dE"cos theta` is the perpendicular component and `"dE"sintheta` is the parallel component.
When the whole wire is considered, the component `"dE"sintheta` is cancelled.
Only the perpendicular component `"dE"cos theta` affects point A.
Hence, effective electric field at point A due to the element dx is dE1.
∴ `"dE"_1 = (lambda"dx" costheta)/(4piin_0("x"^2 + "l"^2))` .............(1)
In `triangle"AZO",`
`tantheta = "x"/"l"`
`"x" = "l" tantheta` ............(2)
On differentiating equation (2), we obtain `("dx")/("d" theta)= "l"sec^2theta`
`"dx" = "l"sec^2theta "d"theta` ........(3)
From equation (2),
`"x"^2 + "l"^2 = "l"^2 + "l"^2 tan theta`
∴ `"l"^2(1 + tan^2 theta) = "l"^2sec^2theta`
∴ `"x"^2 + "l"^2 = "l"^2sin^2theta` ........(4)
Putting equations (3) and (4) in equation (1), we obtain
∴ `"dE"_1= ( lambda "l" sec^2 "d" theta)/(4piin_0"l"^2sec^2 theta) xx costheta`
∴ `"dE"_1 = (lambda cos theta "d" theta)/(4 pi in_0 "l")` ..............(5)
The wire is so long that `theta` tends from `-pi/2` to `+pi/2`.
By integrating equation (5), we obtain the value of field E1 as,
`int_(-pi/2)^(pi/2) "dE"_1 = int_(-pi/2)^(pi/2)lambda/(4piin_0"l") cos theta "d" theta`
`"E"_1 = lambda/(4piin_0"l")[sin theta]_(-pi/2)^(pi/2)`
= `lambda/(4 pi in_0"l") xx 2`
`"E"_1 = lambda/(2piin_0"l")`
Therefore, the electric field due to long wire is `lambda/(2piin_0"l")`.
APPEARS IN
संबंधित प्रश्न
A 36 cm long sonometer wire vibrates with frequency of 280 Hz in fundamental mode, when it is under tension of 24.5 N. Calculate linear density of the material of wire.
Explain why, for a charge configuration, the equipotential surface through a point is normal to the electric field at that point
"For any charge configuration, equipotential surface through a point is normal to the electric field." Justify.
A point charge of 2.0 μC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
A point charge causes an electric flux of −1.0 × 103 Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge.
- If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?
- What is the value of the point charge?
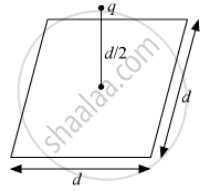
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown the figure. Use Gauss' law to obtain the expression for the electric flux through the square.
Use Gauss' law to derive the expression for the electric field `(vecE)` due to a straight uniformly charged infinite line of charge density λ C/m.
Draw a graph to show the variation of E with perpendicular distance r from the line of charge.
Find the work done in bringing a charge q from perpendicular distance r1 to r2 (r2 > r1)
The electric field intensity outside the charged conducting sphere of radius ‘R’, placed in a medium of permittivity ∈ at a distance ‘r’ from the centre of the sphere in terms of surface charge density σ is
Two wires A and B of the same material and of equal length with the radii in the ratio 1 : 2 are subjected to identical loads. If the length of A increases by 8 mm, then the increase in length of B is:
A spherical ball contracts in volume by 0.02% when subjected to a pressure of 100 atmosphere. Assuming one atmosphere = 105 Nm−2, the bulk modulus of the material of the ball is:
The electric field inside a spherical shell of uniform surface charge density is ______.
What is the nature of the Gaussian surface involved in the Gauss law of electrostatics?
Consider a sphere of radius R with charge density distributed as
ρ(r) = kr for r ≤ R
= 0 for r > R
- Find the electric field at all points r.
- Suppose the total charge on the sphere is 2e where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.
- Obtain the expression for the electric field intensity due to a uniformly charged spherical shell of radius R at a point distant r from the centre of the shell outside it.
- Draw a graph showing the variation of electric field intensity E with r, for r > R and r < R.
A solid metal sphere of radius R having charge q is enclosed inside the concentric spherical shell of inner radius a and outer radius b as shown in the figure. The approximate variation of the electric field `vecE` as a function of distance r from centre O is given by ______.

An infinitely long positively charged straight wire has a linear charge density λ. An electron is revolving in a circle with a constant speed v such that the wire passes through the centre, and is perpendicular to the plane, of the circle. Find the kinetic energy of the electron in terms of the magnitudes of its charge and linear charge density λ on the wire.
Draw a graph of kinetic energy as a function of linear charge density λ.
