Advertisements
Advertisements
प्रश्न
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in Mathematics and Science but not in English
उत्तर
Let the number of students passed in Mathematics M, E be in English and S be in Science.
Then n(U) = 100
n(M) = 12
n(E) = 15
n(S) = 8
n(E ∩ M) = 6
n(M ∩ S) = 7
n(E ∩ S) = 4
And n(E ∩ M ∩ S) = 4
Let us draw a Venn diagram.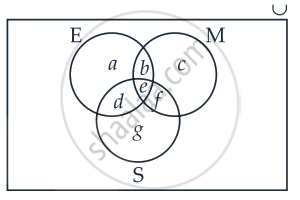
According to the Venn diagram, we get
a + b + d + e = 15 ......(i)
b + c + e + f = 12 ......(ii)
d + e + f + g = 8 .....(iii)
n(E ∩ M) = 6
∴ b + e = 6 ......(iv)
n(M ∩ S) = 7
∴ e + f = 7 ......(v)
n(E ∩ S) = 4
∴ d + e = 4 ......(vi)
And n(E ∩ M ∩ S) = 4
∴ e = 4 ......(vii)
From equation (iv) and (vii)
We get b + 4 = 6
∴ b = 2
From equation (v) and (vii)
We get 4 + f = 7
∴ f = 3
From equation (vi) and (vii)
We get d + 4 = 4
∴ d = 0
From equation (i) we get
a + b + d + e = 15
⇒ a + 2 + 0 + 4 = 15
⇒ a = 9
From equation (ii)
b + c + e + f = 12
⇒ 2 + c + 4 + 3 = 12
⇒ c = 3
From equation (iii)
d + e + f + g = 8
⇒ 0 + 4 + 3 + g = 8
⇒ g = 1
∴ Number of students who passed in Mathematics and Science but not in English, f = 3.
APPEARS IN
संबंधित प्रश्न
Identify whether the following is set or not? Justify your answer.
The collection of questions in this Chapter.
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
5 _____ A
Write the following set in roster form:
A = {x : x is an integer and –3 ≤ x < 7}
Which of the following collection are sets? Justify your answer:
The collection of all question in this chapter.
Describe the following sets in Roster form:
{x ∈ N : x2 < 25};
Describe the following sets in Roster form:
{x ∈ N : x is a prime number, 10 < x < 20};
Describe the following sets in set-builder form:
C = {0, 3, 6, 9, 12, ...}
List all the elements of the following set:
\[B = \left\{ x: x = \frac{1}{2n - 1}, 1 \leq n \leq 5 \right\}\]
List all the elements of the following set:
\[C = \left\{ x: x \text{ is an integer }, - \frac{1}{2} < x < \frac{9}{2} \right\}\]
Write the set of all positive integers whose cube is odd.
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[1 \in A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\phi \in A\]
Let\[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true?
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[2 \subset A\]
What is the total number of proper subsets of a set consisting of n elements?
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
4 _____ A
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
2 _____ A
Describe the following set in Roster form
C = {x/x = 2n + 1, n ∈ N}
A college awarded 38 medals in volleyball, 15 in football, and 20 in basketball. The medals awarded to a total of 58 players and only 3 players got medals in all three sports. How many received medals in exactly two of the three sports?
Answer the following:
Write down the following set in set-builder form
{10, 20, 30, 40, 50}
State which of the following statement are true and which are false. Justify your answer.
37 ∉ {x | x has exactly two positive factors}
Write the following sets in the roaster form:
F = {x | x4 – 5x2 + 6 = 0, x ∈ R}
128 ∈ {y | the sum of all the positive factors of y is 2y}
Determine whether the following statement is true or false. Justify your answer.
For all sets A, B, and C, A – (B – C) = (A – B) – C
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study none of the three languages
Let F1 be the set of parallelograms, F2 the set of rectangles, F3 the set of rhombuses, F4 the set of squares and F5 the set of trapeziums in a plane. Then F1 may be equal to ______.
In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is ______.
A survey shows that 63% of the people watch a News Channel whereas 76% watch another channel. If x% of the people watch both channel, then ______.
