Advertisements
Advertisements
प्रश्न
Take the effect of bulging of earth and its rotation in account. Consider the following statements :
(A) There are points outside the earth where the value of g is equal to its value at the equator.
(B) There are points outside the earth where the value of g is equal to its value at the poles.
विकल्प
Both A and B are correct.
A is correct but B is wrong.
B is correct but A is wrong.
Both A and B are wrong.
उत्तर
A is correct but B is wrong.
We know that the value of acceleration due to gravity decreases when we go up from the surface of the Earth. If we take the into account the effect of bulging of the Earth due to its rotation, we can say that acceleration due to gravity is maximum at the poles and minimum at the equator
So, there are points above both the poles where the value of g is equal to its value at the equator.
APPEARS IN
संबंधित प्रश्न
Is there any meaning of "Weight of the earth"?
An apple falls from a tree. An insect in the apple finds that the earth is falling towards it with an acceleration g. Who exerts the force needed to accelerate the earth with this acceleration g?
The acceleration of the moon just before it strikes the earth in the previous question is
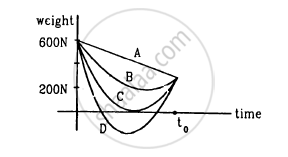
Suppose, the acceleration due to gravity at the earth's surface is 10 m s−2 and at the surface of Mars it is 4⋅0 m s−2. A 60 kg passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky. Which part of the following figure best represents the weight (net gravitational force) of the passenger as a function of time?
If the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body of mass m from the earth's surface to a height R equal to the radius of the earth is
What is the acceleration due to gravity on the top of Mount Everest? Mount Everest is the highest mountain peak of the world at the height of 8848 m. The value at sea level is 9.80 m s−2.
A body is weighed by a spring balance to be 1.000 kg at the North Pole. How much will it weigh at the equator? Account for the earth's rotation only.
A particle is fired vertically upward with a speed of 15 km s−1. With what speed will it move in interstellar space. Assume only earth's gravitational field.
Explain the variation of g with latitude.
Explain the variation of g with depth from the Earth’s surface.
Suppose we go 200 km above and below the surface of the Earth, what are the g values at these two points? In which case, is the value of g small?
If both the mass and the radius of the earth decrease by 1%, then the value of acceleration due to gravity will
One can easily weigh the earth by calculating the mass of the earth by using the formula:
Which of the following options are correct?
- Acceleration due to gravity decreases with increasing altitude.
- Acceleration due to gravity increases with increasing depth (assume the earth to be a sphere of uniform density).
- Acceleration due to gravity increases with increasing latitude.
- Acceleration due to gravity is independent of the mass of the earth.
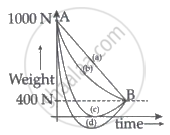
A person whose mass is 100 kg travels from Earth to Mars in a spaceship. Neglect all other objects in the sky and take acceleration due to gravity on the surface of the Earth and Mars as 10 m/s2 and 4 m/s2 respectively. Identify from the below figures, the curve that fits best for the weight of the passenger as a function of time.
If R is the radius of the earth and g is the acceleration due to gravity on the earth's surface, the mean density of the earth is ______.
A ball is immersed in water kept in container and released. At the same time container is accelerated in horizontal direction with acceleration, `sqrt44` m/s2. Acceleration of ball w.r.t. container is ______ m/s2 (specific gravity of ball = 12/17, g = 10 m/s2)
The percentage decrease in the weight of a rocket, when taken to a height of 32 km above the surface of the earth will, be ______.
(Radius of earth = 6400 km)
