Advertisements
Advertisements
प्रश्न
Point P(x, 4) lies on the line segment joining the points A(−5, 8) and B(4, −10). Find the ratio in which point P divides the line segment AB. Also find the value of x.
उत्तर
Let point P (x, 4) divide line segment AB in the ratio K:1.
Coordinates of A = (−5, 8)
Coordinates of B = (4, −10)
On using section formula, we obtain
`(x,4)=((kxx4+1xx(-5))/(k+1))((kxx(-10)+1xx8)/(k+1))`
`(x,4)=((4k-5)/(k+1),(-10k+8)/(k+1))`
`rArr(4k-5)/(k+1)=x`........................(1)
`and (-10k+8)/(k+1)=4..................(2)
From equation (2):
− 10K + 8 = 4(K + 1)
⇒ − 10K + 8 = 4K + 4
⇒ 14K = 4
`rArr K =2/7`
Thus, point P divides AB in the ratio `2/7 : ie ., 2:7.`
From equation (1):
`(4xx2/7-5)/(2/7+1)=x`
`(-27/7)/(9/7)=x`
`x=-3`
APPEARS IN
संबंधित प्रश्न
How will you describe the position of a table lamp on your study table to another person?
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross- streets in your model. A particular cross-street is made by two streets, one running in the North - South direction and another in the East - West direction. Each cross street is referred to in the following manner : If the 2nd street running in the North - South direction and 5th in the East - West direction meet at some crossing, then we will call this cross-street (2, 5). Using this convention, find:
- how many cross - streets can be referred to as (4, 3).
- how many cross - streets can be referred to as (3, 4).
Find the distance between the following pair of points:
(a, 0) and (0, b)
Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
Name the quadrilateral formed, if any, by the following points, and given reasons for your answers:
A(-3, 5) B(3, 1), C (0, 3), D(-1, -4)
Name the quadrilateral formed, if any, by the following points, and given reasons for your answers:
A(4, 5) B(7, 6), C (4, 3), D(1, 2)
If the point A (4,3) and B ( x,5) lies on a circle with the centre o (2,3) . Find the value of x.
Show that the following points are the vertices of a rectangle
A (0,-4), B(6,2), C(3,5) and D(-3,-1)
The line segment joining A( 2,9) and B(6,3) is a diameter of a circle with center C. Find the coordinates of C
If the points P (a,-11) , Q (5,b) ,R (2,15) and S (1,1). are the vertices of a parallelogram PQRS, find the values of a and b.
Find the area of the triangle formed by joining the midpoints of the sides of the triangle whose vertices are A(2,1) B(4,3) and C(2,5)
Points A(-1, y) and B(5,7) lie on the circle with centre O(2, -3y).Find the value of y.
The distance of the point P (4, 3) from the origin is
If the point P(x, 3) is equidistant from the point A(7, −1) and B(6, 8), then find the value of x and find the distance AP.
If x is a positive integer such that the distance between points P (x, 2) and Q (3, −6) is 10 units, then x =
The line segment joining points (−3, −4), and (1, −2) is divided by y-axis in the ratio.
What is the form of co-ordinates of a point on the X-axis?
If the sum of X-coordinates of the vertices of a triangle is 12 and the sum of Y-coordinates is 9, then the coordinates of centroid are ______
The coordinates of a point whose ordinate is `-1/2` and abscissa is 1 are `-1/2, 1`.
A tiling or tessellation of a flat surface is the covering of a plane using one or more geometric shapes, called tiles, with no overlaps and no gaps. Historically, tessellations were used in ancient Rome and in Islamic art. You may find tessellation patterns on floors, walls, paintings etc. Shown below is a tiled floor in the archaeological Museum of Seville, made using squares, triangles and hexagons.

A craftsman thought of making a floor pattern after being inspired by the above design. To ensure accuracy in his work, he made the pattern on the Cartesian plane. He used regular octagons, squares and triangles for his floor tessellation pattern
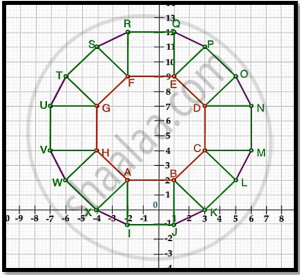
Use the above figure to answer the questions that follow:
- What is the length of the line segment joining points B and F?
- The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the coordinates of Z?
- What are the coordinates of the point on y-axis equidistant from A and G?
OR
What is the area of Trapezium AFGH?
