Advertisements
Advertisements
प्रश्न
`p/q` के रूप में 1.999... का मान, जहाँ p और q पूर्णांक हैं तथा q ≠ 0, होगा :
विकल्प
`19/10`
`1999/1000`
2
`1/9`
उत्तर
2
स्पष्टीकरण -
माना x = 1.999... (i)
(i) को 10 से गुणा करने पर हमें प्राप्त होता है।
10x = 19.999... (ii)
(i) को (ii) से घटाने पर, हमें प्राप्त होता है।
10x – x = (19.999...) – (1.9999...)
⇒ 9x = 18
∴ x = 2
APPEARS IN
संबंधित प्रश्न
सिद्ध कीजिए कि `3 + 2sqrt5` एक अपरिमेय संख्या है।
सिद्ध कीजिए कि निम्नलिखित संख्या अपरिमेय हैं:
`7sqrt5`
नीचे दिए गए कथन सत्य हैं या असत्य हैं। कारण के साथ अपने उत्तर दीजिए।
प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
दिखाइए कि संख्या रेखा पर `sqrt5` को किस प्रकार निरूपित किया जा सकता है।
सिद्ध कीजिए कि `sqrt3` + `sqrt5` एक अपरिमेय संख्या है।
संख्या `sqrt(2)` का दशमलव प्रसार है :
निम्नलिखित में से कौन-सी एक अपरिमेय संख्या है?
`2sqrt(3) + sqrt(3)` बराबर है :
मान लीजिए कि x और y क्रमशः परिमेय और अपरिमेय संख्याएँ हैं। क्या x + y आवश्यक रूप से एक अपरिमेय संख्या है? अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
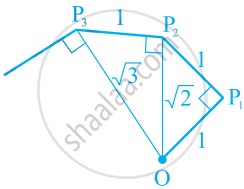
कक्षा के लिए क्रियाकलाप (वर्गमूल सर्पिल की रचना): कागज की एक बड़ी शीट लीजिए और नीचे दी गई विधि से “वर्गमूल सर्पिल” (square root spiral) की रचना कीजिए। सबसे पहले एक बिन्दु O लीजिए और एकक लंबाई का रेखाखंड (line segment) OP खींचिए। एकक लंबाई वाले OP1 पर लंब रेखाखंड P1P2 खींचिए। अब OP2, पर लंब रेखाखंड P2P3 खींचिए। तब OP3 पर लंब रेखाखंड P3P4 खींचिए। इस प्रक्रिया को जारी रखते हुए OPn–1 पर एकक लंबाई वाला लंब रेखाखंड खींचकर आप रेखाखंड Pn–1Pn प्राप्त कर सकते हैं। इस प्रकार आप बिन्दु O, P1, P2, P3,..., Pn,... प्राप्त कर लेंगे और उन्हें मिलाकर `sqrt2, sqrt3, sqrt4...` को दर्शाने वाला एक सुंदर सर्पिल प्राप्त कर लेंगे।