Advertisements
Advertisements
प्रश्न
Prove that the points (0 , 2) , (1 , 1) , (4 , 4) and (3 , 5) are the vertices of a rectangle.
उत्तर
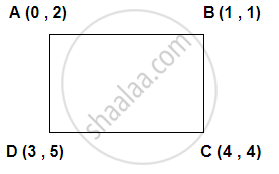
AB = `sqrt ((0 - 1)^2 + (2 - 1)^2) = sqrt 2` units
BC = `sqrt ((1 - 4)^2 + (1 - 4)^2) = 3 sqrt 2` units
CD = `sqrt ((4 - 3)^2 + (4 - 5)^2) = sqrt 2` units
DA = `sqrt ((3 - 0)^2 + (5 - 2)^2) = 3 sqrt 2` units
AC = `sqrt ((4 - 0)^2 + (4 - 2)^2) = sqrt 20 = 2 sqrt 5` units
BC = `sqrt ((3 - 1)^2 + (5 - 1)^2) = sqrt 20 = 2 sqrt 5` units
∵ AB = CD and BC = DA
Also , AC = BD
∴ ABCD is a rectangle.
APPEARS IN
संबंधित प्रश्न
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
Name the type of quadrilateral formed, if any, by the following point, and give reasons for your answer:
(−3, 5), (3, 1), (0, 3), (−1, −4)
The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end.
Find the distance between the points
(i) A(9,3) and B(15,11)
Distance of point (-3, 4) from the origin is .....
(A) 7 (B) 1 (C) 5 (D) 4
A(2, 5), B(-2, 4) and C(-2, 6) are the vertices of a triangle ABC. Prove that ABC is an isosceles triangle.
The centre of a circle is (2x - 1, 3x + 1). Find x if the circle passes through (-3, -1) and the length of its diameter is 20 unit.
Show that the quadrilateral with vertices (3, 2), (0, 5), (- 3, 2) and (0, -1) is a square.
If the distance between point L(x, 7) and point M(1, 15) is 10, then find the value of x
Show that points A(–1, –1), B(0, 1), C(1, 3) are collinear.
