Advertisements
Advertisements
प्रश्न
Prove that
Refractive index = `"Real depth"/"Apparent depth"`
उत्तर
In the given figure,
In rt. Δ DKA
Sin i = `("DK")/("AD")`
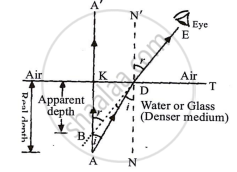
In rt. Δ DKB, Sin r = `("DK")/("BD")`
`""_mmu_a ∴ sin i/sin r = ("DK"/"AD")/("DK"/"BD")`
`sin i/sin r = "BD"/"AD"`
Or `""_amu_m = 1/(""_mmu_a)`
`""_amu_m = "AD"/"BD"`
Since point D is very close to K
`""_amu_m = "AK"/"K"`
`""_amu_m = "Real depth"/"Apparent depth"`
APPEARS IN
संबंधित प्रश्न
How is the refractive index of a material related to real and apparent depth?
How is the refractive index of a medium related to the real and apparent depths of an object in that medium?
Water in a pond appears to be only three-quarters of its actual depth.
- What property of light is responsible for this observation? Illustrate your answer with the help of a ray diagram.
- How is the refractive index of water calculated from its real and apparent depth?
A student puts his pencil into an empty trough and observes the pencil from the position as indicated in

- What change will be observed in the appearance of the pencil when water is poured into the trough?
- Name the phenomenon which accounts for the above stated observation.
- Complete the diagram showing how the student’s eye sees the pencil through water.
Show the path of a ray of light when it travels from air into water, the angle of incidence being 30°. Mark the angle of incidence and the corresponding angle of refraction.
How are the refractive index of water-related to the real depth and the apparent depth of a column of water?
With the help of a well-labelled diagram show that the apparent depth of an object, such as a coin, in water is less than its real depth.
A coin kept inside water [µ = 4/3] when viewed from air in a vertical direction appears to be raised by 3.0 mm. Find the depth of the coin in water.
A water pond appears to be 3 m deep. If the refractive index of water is 4/3, find the actual depth of the pond.
A coin is placed at the bottom of a beaker containing water (refractive index = 4/3) at a depth of 16 cm. By what height the coin appears to be raised when seen from vertically above?
