Advertisements
Advertisements
प्रश्न
Water in a pond appears to be only three-quarters of its actual depth.
- What property of light is responsible for this observation? Illustrate your answer with the help of a ray diagram.
- How is the refractive index of water calculated from its real and apparent depth?
उत्तर
Light has a feature called refraction, which states that "light bends away from normal when it travels from a denser medium to a rarer medium."
Real-depth AK observed depth BK, BK < AK
Because of this, the water looks shallower than it actually is.
Refractive index of water = `"real depth"/"apparent depth"`
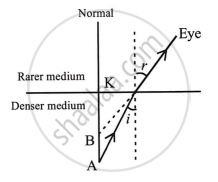
real depth = 1m
Apparent depth = `3/4` m
`mu "water" = 1/(3/4) = 4/3`
μ water = 1.33
APPEARS IN
संबंधित प्रश्न
How is the refractive index of a material related to real and apparent depth?
How is the refractive index of a medium related to the real and apparent depths of an object in that medium?
Prove that
Refractive index = `"Real depth"/"Apparent depth"`
An object placed in one medium when seen from the other medium, appears to be vertically shifted. Name two factors on which the magnitude of shift depends and state how does it depend on them.
Show the path of a ray of light when it travels from air into water, the angle of incidence being 30°. Mark the angle of incidence and the corresponding angle of refraction.
How are the refractive index of water-related to the real depth and the apparent depth of a column of water?
With the help of a well-labelled diagram show that the apparent depth of an object, such as a coin, in water is less than its real depth.
A coin kept inside water [µ = 4/3] when viewed from air in a vertical direction appears to be raised by 3.0 mm. Find the depth of the coin in water.
A water pond appears to be 3 m deep. If the refractive index of water is 4/3, find the actual depth of the pond.
A coin is placed at the bottom of a beaker containing water (refractive index = 4/3) at a depth of 16 cm. By what height the coin appears to be raised when seen from vertically above?
