Advertisements
Advertisements
Question
Water in a pond appears to be only three-quarters of its actual depth.
- What property of light is responsible for this observation? Illustrate your answer with the help of a ray diagram.
- How is the refractive index of water calculated from its real and apparent depth?
Solution
Light has a feature called refraction, which states that "light bends away from normal when it travels from a denser medium to a rarer medium."
Real-depth AK observed depth BK, BK < AK
Because of this, the water looks shallower than it actually is.
Refractive index of water = `"real depth"/"apparent depth"`
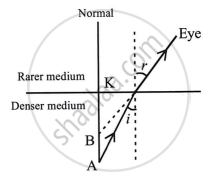
real depth = 1m
Apparent depth = `3/4` m
`mu "water" = 1/(3/4) = 4/3`
μ water = 1.33
APPEARS IN
RELATED QUESTIONS
How is the refractive index of a material related to real and apparent depth?
How is the refractive index of a medium related to the real and apparent depths of an object in that medium?
Prove that
Refractive index = `"Real depth"/"Apparent depth"`
A student puts his pencil into an empty trough and observes the pencil from the position as indicated in

- What change will be observed in the appearance of the pencil when water is poured into the trough?
- Name the phenomenon which accounts for the above stated observation.
- Complete the diagram showing how the student’s eye sees the pencil through water.
An object placed in one medium when seen from the other medium, appears to be vertically shifted. Name two factors on which the magnitude of shift depends and state how does it depend on them.
Show the path of a ray of light when it travels from air into water, the angle of incidence being 30°. Mark the angle of incidence and the corresponding angle of refraction.
With the help of a well-labelled diagram show that the apparent depth of an object, such as a coin, in water is less than its real depth.
A coin kept inside water [µ = 4/3] when viewed from air in a vertical direction appears to be raised by 3.0 mm. Find the depth of the coin in water.
A water pond appears to be 3 m deep. If the refractive index of water is 4/3, find the actual depth of the pond.
A coin is placed at the bottom of a beaker containing water (refractive index = 4/3) at a depth of 16 cm. By what height the coin appears to be raised when seen from vertically above?
