Advertisements
Advertisements
प्रश्न
Represent the truth of the following statement by the Venn diagram.
If a quadrilateral is a rhombus, then it is a parallelogram.
उत्तर
Let U : The set of all quadrilaterals.
P : The set of all parallelograms.
R : The set of all rhombuses.
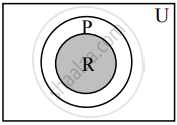
The above Venn diagram represents truth of the given statement, R ⊂ P.
APPEARS IN
संबंधित प्रश्न
Draw appropriate Venn diagram for the following:
A' ∩ B'
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
If A and B are two sets such that \[A \subset B\] then find:
\[A \cup B\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find\[B \cup D\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[A \cup B \cup C\]
If A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}, find:
\[\left( A \cup D \right) \cap \left( B \cup C \right)\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\]and D = {x : x is a prime natural number}. Find: \[A \cap B\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap C\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[B \cap D\]
Let \[A = \left\{ x: x \in N \right\}, B = \left\{ x: x - 2n, n \in N \right\}, C = \left\{ x: x = 2n - 1, n \in N \right\}\] and D = {x : x is a prime natural number}. Find: \[C \cap D\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - B\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}. Find: \[A - D\]
Let A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}.
Find: \[B - D\]
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that \[\left( A \cup B \right)' = A' \cap B'\]
- show the sets U, P and P' by the Venn diagram.
- Verify (P')' = P
Represent the union of two sets by Venn diagram for the following.
A = {3, 4, 5, 7} B = {1, 4, 8}
Using the Venn diagram, examine the logical equivalence of the following statements:
(a) Some politicians are actors.
(b) There are politicians who are actors.
(c) There are politicians who are not actors.
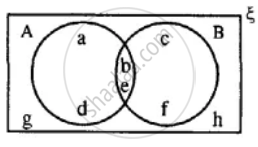
From the given diagram, find:
(i) A’
(ii) B’
(iii) A' ∪ B'
(iv) (A ∩ B)'
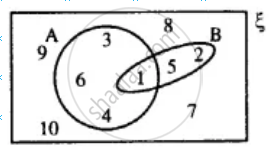
Is A' ∪ B' = (A ∩ B)' ?
Also, verify if A' ∪ B' = (A ∩ B)'.
Use the given Venn-diagram to find:
B - A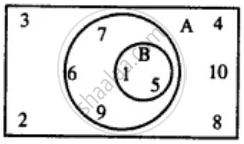
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
A ∪ B
Draw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
B - A
Draw a Venn-diagram to show the relationship between two sets A and B; such that A ⊆ B, Now shade the region representing :
(A ∪ B)'
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
(A ∪ B)'
Two sets A and B are such that A ∩ B = Φ. Draw a venn-diagram to show the relationship between A and B. Shade the region representing :
B - A
In the given diagram, shade the region which represents the set given underneath the diagrams: (A ∩ B)'
From the given diagram, find :
(i) (A ∪ B) - C
(ii) B - (A ∩ C)
(iii) (B ∩ C) ∪ A
Verify :
A - (B ∩ C) = (A - B) ∪ (A - C)

Using the given diagram, express the following sets in the terms of A and B. {a, d, g, h}
Represent the truth of the following statement by the Venn diagram.
Some hardworking students are obedient.
Represent the truth of the following statement by the Venn diagram.
No circles are polygons.
Represent the following statement by the Venn diagram.
If n is a prime number and n ≠ 2, then it is odd.
Draw Venn diagram for the following:
Some students are not scholars
Take the set of natural numbers from 1 to 20 as universal set and show set X using Venn diagram.
X = {x | x ∈ N, and 7 < x < 15}
