Advertisements
Advertisements
प्रश्न
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If price increases, then demand falls.
उत्तर
Let p : Prince increases.
q : demand falls.
The given statement is p → q.
But p → q ≡ ~p ∨ q.
The given statement can be written as ‘Price does not increase or demand falls’.
Notes
The answer in the textbook is incorrect.
APPEARS IN
संबंधित प्रश्न
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Write converse, inverse contrapositive of the statement "If two triangles are not congruent then their areas are not equal.
Write the following compound statement symbolically.
x is not irrational number but is a square of an integer.
Construct the truth table of the following statement pattern.
[p → (q → r)] ↔ [(p ∧ q) → r]
Construct the truth table of the following:
∼ (∼p ∧ ∼q) ∨ q
Express the following statement in symbolic form.
Mango is a fruit but potato is a vegetable.
Write the negation of the following statement.
It is false that Nagpur is capital of Maharashtra
Write the negation of the following statement.
2 + 3 ≠ 5
Write the truth value of the negation of the following statement.
`sqrt5` is an irrational number.
Write the following statement in symbolic form.
If Kutub-Minar is in Delhi then Taj-Mahal is in Agra.
Find the truth value of the following statement.
It is not true that 3 − 7i is a real number.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ↔ ~(p ∨ q)
Fill in the blanks :
Conjunction of two statement p and q is symbolically written as ______.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Mona likes Mathematics and Physics.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
3 is prime number if 3 is perfect square number.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that Ram is tall and handsome.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that intelligent persons are neither polite nor helpful.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
Proof is lengthy and it is not interesting.
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
If proof is lengthy then it is interesting.
Write the negation of the following.
Ramesh is intelligent and he is hard working.
Write the negation of the following.
Kanchanganga is in India and Everest is in Nepal.
Rewrite the following statement without using the connective ‘If ... then’.
If a quadrilateral is rhombus then it is not a square.
Rewrite the following statement without using the connective ‘If ... then’.
If it rains then the principal declares a holiday.
Write the negation of the following statement.
10 > 5 and 3 < 8
Write the negation of the following statement.
∃ x ∈ A, such that x + 5 < 11.
If p → q is an implication, then the implication ∼ q → ∼ p is called its
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Write the negation of p → q
Choose the correct alternative:
Negation of p → (p ˅ ~q) is
Choose the correct alternative:
A biconditional statement is the conjunction of two ______ statements
State whether the following statement is True or False:
The converse of inverse of ~ p → q is q → ~ p
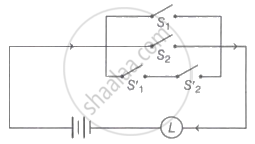
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
The Boolean expression ∼(q ⇒ ∼p) is equivalent to: ______
The negation of ∼s ∨ (∼r ∧ s) is equivalent to ______
The statement ∼(p ↔ ∼q) is ______.
From the following set of statements, select two statements which have similar meaning.
- If a man is judge, then he is honest.
- If a man is not a judge, then he is not honest.
- If a man is honest, then he is a judge.
- If a man is not honest, then he is not a judge.
