Advertisements
Advertisements
प्रश्न
Show that intensity of electric field at a point in broadside position of an electric dipole is given by:
E = `(1/(4piepsilon_0)) "p"/(("r"^2 + l^2)^(3//2))`
Where the terms have their usual meaning.
उत्तर
Electric field due to dipole (broadside on position)
Consider dipole of length 2l and moment `vecp`.
From the figure, resultant electric field intensity at C:
`vec"E" = vec"E"_"A" + vec"E"_"B"`
`|vec"E"_"A"| = 1/(4piepsilon_0) "q"/("r"^2 + l^2)`
`|vec"E"_"B"| = 1/(4piepsilon_0) "q"/("r"^2 + l^2)`
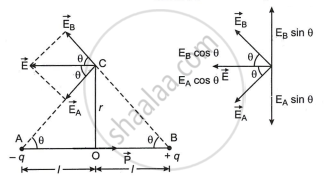
Sine components of `vec"E"_"A" "and" vec"E"_"B"` get cancelled each other as `|vec"E"_"A"| = |vec"E"_"B"|`.
The cosine components get added up to give the resultant field.
i.e., E = EA cos θ + EB cos θ
`= 1/(4piepsilon_0) * "q"/("r"^2 + l^2) cos theta + 1/(4piepsilon_0) * "q"/("r"^2 + l^2) cos theta`
`= 2 * 1/(4piepsilon_0) * "q"/("r"^2 + l^2) cos theta`
`= 2 xx 1/(4piepsilon_0) * "q"/("r"^2 + l^2) xx l/("r"^2 + l^2)^(1//2)`
`= 1/(4piepsilon_0) ("q"(2l))/(("r"^2 + l^2)^(3//2))`
E = `1/(4piepsilon_0) "p"/(("r"^2 + l^2)^(3//2))` as p = q(2l)
The above expression gives the magnitude of the field. The direction of electric field E at C is opposite to the direction of the dipole moment `vec"p"`.
APPEARS IN
संबंधित प्रश्न
An electric dipole of dipole moment`vecp` consists of point charges +q and −q separated by a distance 2a apart. Deduce the expression for the electric field `vecE` due to the dipole at a distance x from the centre of the dipole on its axial line in terms of the dipole moment `vecp`. Hence show that in the limit x>> a, `vecE->2vecp"/"(4piepsilon_0x^3)`
A short electric dipole (which consists of two point charges, +q and -q) is placed at the centre 0 and inside a large cube (ABCDEFGH) of length L, as shown in Figure 1. The electric flux, emanating through the cube is:
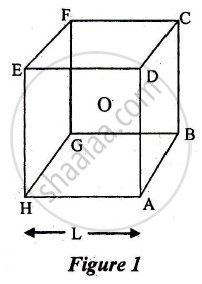
a) `q"/"4piin_9L`
b) zero
c) `q"/"2piin_0L`
d) `q"/"3piin_0L`
An electric dipole of length 2 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of \[8\sqrt{3}\] Nm. Calculate the potential energy of the dipole, if it has a charge \[\pm\] 4 nC.
Two particles, carrying charges −q and +q and and of mass m each, are fixed at the ends of a light rod of length a to form a dipole. The rod is clamped at an end and is placed in a uniform electric field E with the axis of the dipole along the electric field. The rod is slightly tilted and then released. Neglecting gravity, find the time period of small oscillations.
When an electric dipole p is placed in a uniform electric field E then at what angle the value of torque will be maximum?
On the axis and on the equator of an electric dipole for all points ____________.
Electric charges q, q, - 2q are placed at the comers of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is ____________.
An electric dipole of moment `vec"p"` is placed normal to the lines of force of electric intensity `vec"E"`, then the work done in deflecting it through an angle of 180° is:
