Advertisements
Advertisements
Question
Show that intensity of electric field at a point in broadside position of an electric dipole is given by:
E = `(1/(4piepsilon_0)) "p"/(("r"^2 + l^2)^(3//2))`
Where the terms have their usual meaning.
Solution
Electric field due to dipole (broadside on position)
Consider dipole of length 2l and moment `vecp`.
From the figure, resultant electric field intensity at C:
`vec"E" = vec"E"_"A" + vec"E"_"B"`
`|vec"E"_"A"| = 1/(4piepsilon_0) "q"/("r"^2 + l^2)`
`|vec"E"_"B"| = 1/(4piepsilon_0) "q"/("r"^2 + l^2)`
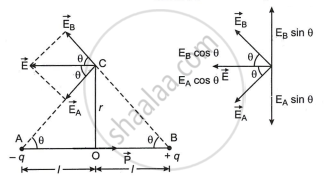
Sine components of `vec"E"_"A" "and" vec"E"_"B"` get cancelled each other as `|vec"E"_"A"| = |vec"E"_"B"|`.
The cosine components get added up to give the resultant field.
i.e., E = EA cos θ + EB cos θ
`= 1/(4piepsilon_0) * "q"/("r"^2 + l^2) cos theta + 1/(4piepsilon_0) * "q"/("r"^2 + l^2) cos theta`
`= 2 * 1/(4piepsilon_0) * "q"/("r"^2 + l^2) cos theta`
`= 2 xx 1/(4piepsilon_0) * "q"/("r"^2 + l^2) xx l/("r"^2 + l^2)^(1//2)`
`= 1/(4piepsilon_0) ("q"(2l))/(("r"^2 + l^2)^(3//2))`
E = `1/(4piepsilon_0) "p"/(("r"^2 + l^2)^(3//2))` as p = q(2l)
The above expression gives the magnitude of the field. The direction of electric field E at C is opposite to the direction of the dipole moment `vec"p"`.
APPEARS IN
RELATED QUESTIONS
Derive an expression for the intensity of electric field at a point in broadside position or on [4)
an equatorial line of an electric dipole.
An electric dipole of length 2 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of \[8\sqrt{3}\] Nm. Calculate the potential energy of the dipole, if it has a charge \[\pm\] 4 nC.
Define electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
A uniform electric field is prevailing in X - direction in certain region. The coordinates of points P, Q, and R are (0, 0), (2, 0) and (0, 2) respectively. Which of the following alternatives is true for the potentials at these points?
A metal sphere of radius 1 cm is given a charge of 3.14 µC. Find the electric intensity at a distance of 1 m from the centre of sphere.
`[epsilon_0 = 8.85 xx 10^-12 "F"//m]`
When an electric dipole p is placed in a uniform electric field E then at what angle the value of torque will be maximum?
Electric charges q, q, - 2q are placed at the comers of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is ____________.
Polar molecules are the molecules ______.
